これで掛谷の問題は終わった…と思われた

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

しかし、掛谷の問題はこれで終わりというわけではなかった。

星状領域を考えると事情は全く異なっていて、「限りなく０に近づける」ことは可能ではないのである。

定理(Cunnigham,1971)

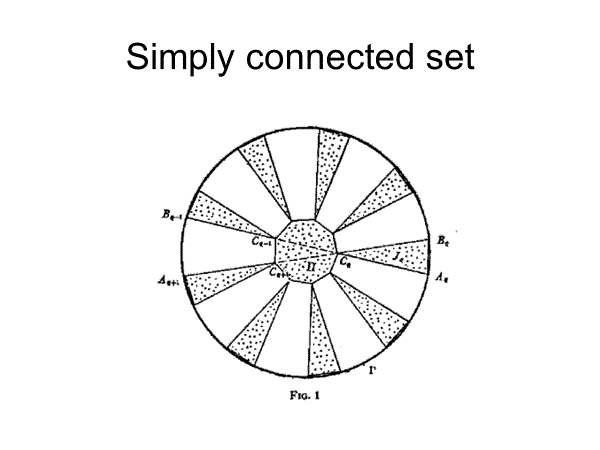
For given ε>0, there exists simply connected Kakeya set of area less than ε contained in unit circle. (Besicovitch type theorem for simply connected Kakeya set) For star shaped set, ‘arbitrarily small area’ is not true.

星状領域とはたとえは中心にいる観測者が領域内のすべての点を観測することができるものであって、それに対して単連結領域はそれが可能でないものを指す。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝