ところが、その予想に反して、１９２７年、ベシコヴィッチが面積を限りなく０に近づけることのできる図形を構成した。

驚愕の結果であった。この直観に反する結果はベシコヴィッチ・ショックと呼んでよいものであろう。

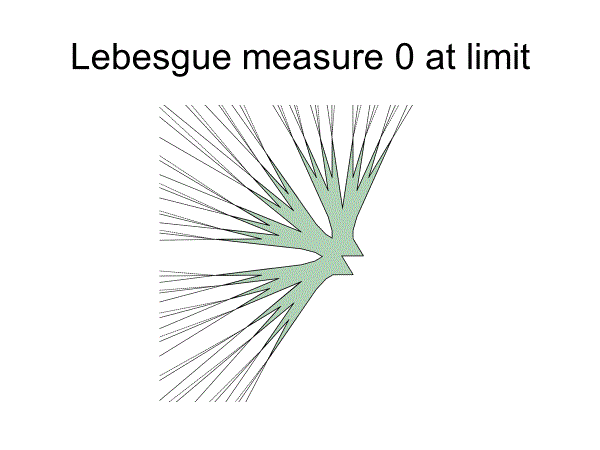
定理(Besicovitch,1927)

For given ε>0, there exists Kakeya set of area less than ε.

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

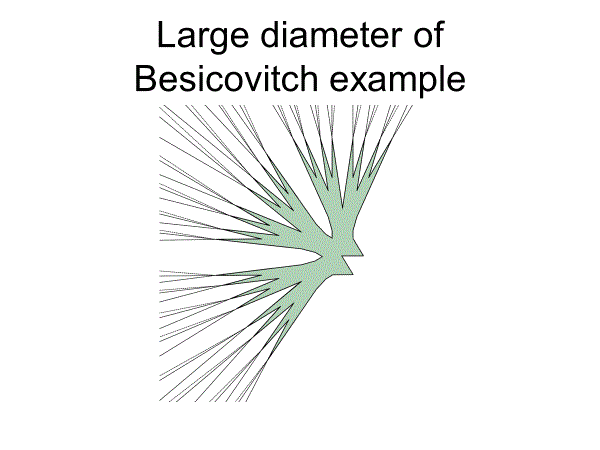
とはいっても、ベシコヴィッチ集合の直径は巨大なものになってしまう。

もし、集合の直径を有限の円に制限したらこの定理は成立しないのでは・・・と考えるのは自然な発想であろう。

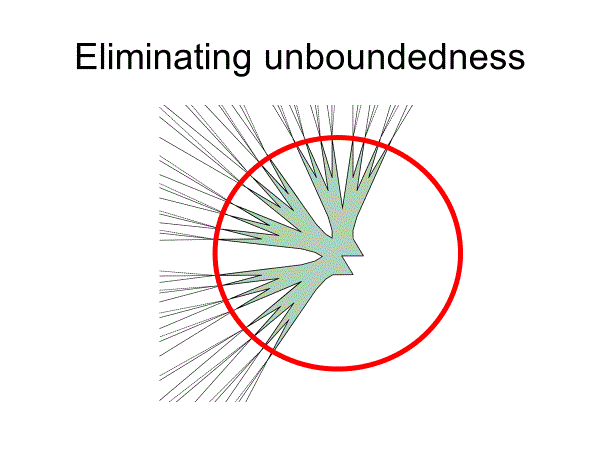
ところが、有限円に制限しても同様の定理ば成り立ってしまう。

定理(van Alphen,1941)

For given ε>0, there exists Kakeya set of area less than ε contained inside a circle of radius 2+ε. (circle version of Besicovitch type theorem)

しかも、この定理は後年、単位円にまで改良されてしまうのであった。

定理(Cunnigham,1971)

Improved to simply connected Kakeya set of area less than ε contained inside a circle of radius 1

これで掛谷の問題は終わった…

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝