■バラ曲線の等分問題(その11)
サイクロイド曲線はバラ曲線同様、代数曲線である(サイクロイドは代数曲線ではない)
カージオイドは任意等分可能であるが、一般のサイクロイド曲線族ではどうか?
===================================
答えを先にいうと・・・
カージオイド(n=1)は任意等分可
円(n=2)、レムニスケート(n=4)は2^k等分・フェルマー素数等分可
三葉曲線(n=3)、六葉曲線(n=6)は2^k等分可
五葉曲線(n=5)は等分不可
に対して、サイクロイド曲線族は任意等分可(以下の図には2等分点のみを示す)
===================================
[1]サイクロイドの2等分点, y=3/2
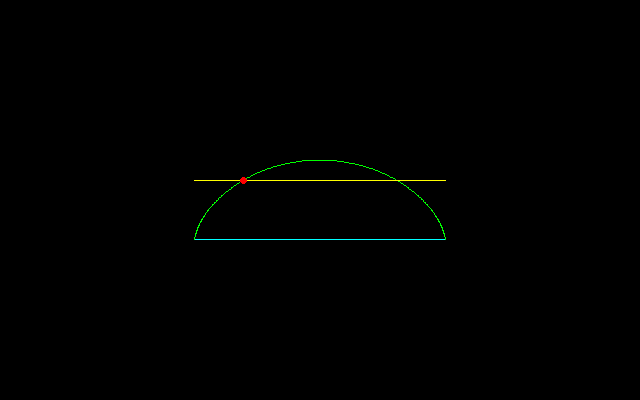
===================================
[2]デルトイド・アステロイドの2等分点, r=√(n^2-3n+3)
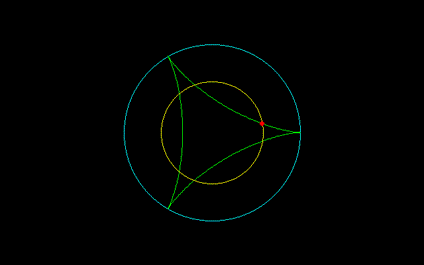
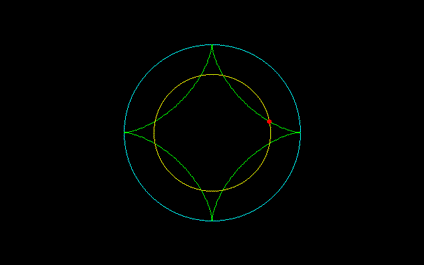
===================================
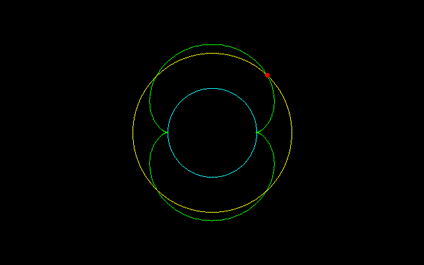
[3]カージオイド・ネフロイドの2等分点, r=√(n^2+3n+3)
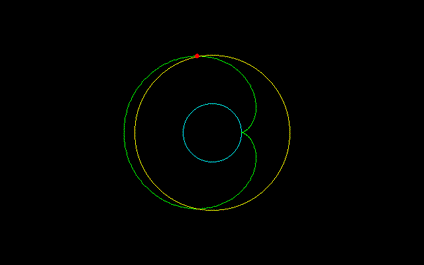
===================================







