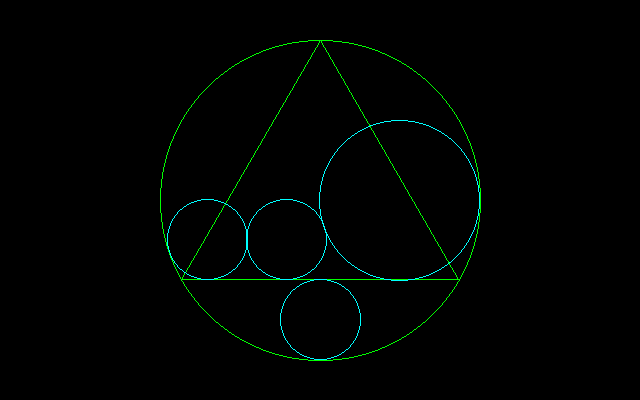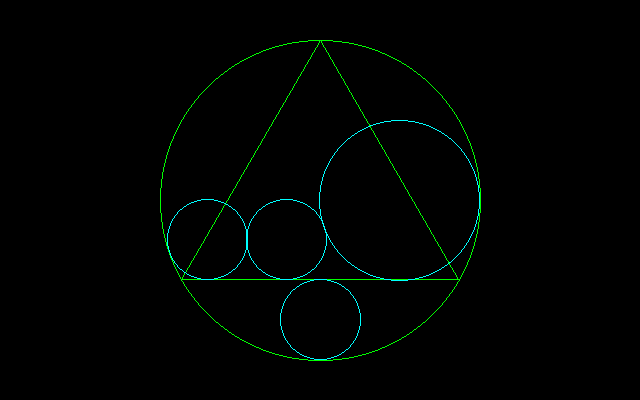図形の問題では座標を設定して，どうしても計算したくなるものであるが，

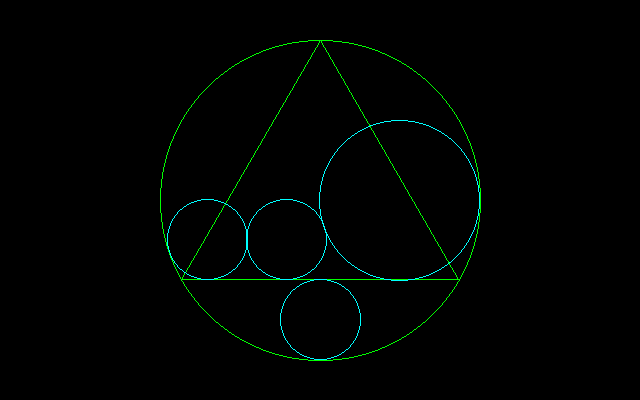
　　［Ｑ］中円の半径は？

のようにほとんど計算しなくてもよい問題もあるようだ．

　これ以外にも，同心円に関する問題ではしばしば「計算してはならない問題」がある．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［Ｑ１］同一の円に内接・外接する２つの正六角形を考える．小さい正六角形の面積が３のとき，大きい正六角形の面積は？

［Ａ１］小さい正六角形の頂点と大きい正六角形の辺の中点が一致するように，外側の正六角形を回転させる．次に円の中心と内側の正六角形の頂点を結び，内側の正六角形を正三角形で６等分する．さらに正三角形の重心と頂点を結び，内角３０°，３０°，１２０°の二等辺三角形で内側の正六角形を１８等分する．

　このように線でわけると「麻の葉文様」の２４個の合同な三角形ができる．そのうち１８個が小さな正六角形を形作る．面積比は１８：２４＝３：４であるから，大きい正六角形の面積は４となる．この問題に三角関数は不要であって，計算してはならない問題なのである．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［Ｑ２］１辺の長さが２の正方形に内接する正十二角形の面積は？

［Ａ２］２×２正方形は１６個の合同な正三角形と３２個の合同な二等辺三角形（内角１５°，１５°，１５０°）に分割される．正十二角形は１２個の正三角形と２４個の二等辺三角形により形作られる．したがって，この正十二角形の面積は３である．すなわち，半径１の円に内接する正十二角形の面積は３であるという円周率πの近似を与えていることになる．

　この問題は１８９８年にハンガリーの数学者キルシェクにより十二角形の面積が決定されたもので「キルシェクのタイル」と呼ばれる．正方形の中に各辺を１辺とする正三角形を４個作る．次に正三角形の頂点で正方形の中にあるもの同士を結んで正方形を作る．すると，正方形の各辺の中点４個と４つの正三角形の交点８個で正十二角形ができる．このように，正三角形の頂点を結んで作られた正方形と正十二角形がキルシェクのタイルの基本形となる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝