試しにアルキメデスらせん上にα=137.5°で点配置すると中心部に集中することが見て取れるだろう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

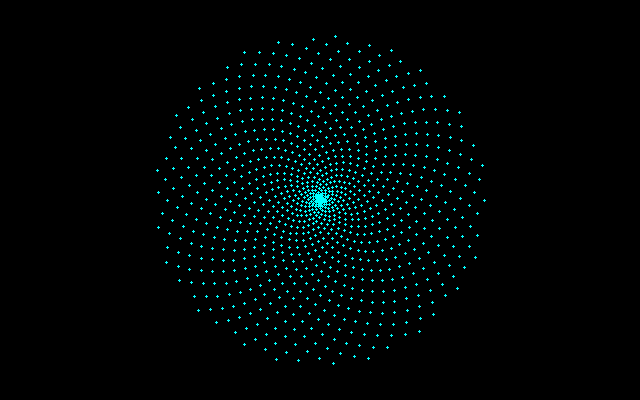
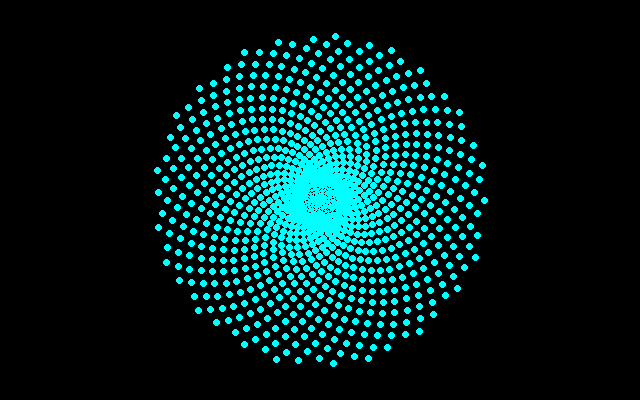
それに対してフェルマーらせん上ににα=137.5°で点配置すると

不即不離で準結晶的 (Delone set)

Voronoi領域の面積がほぼ一定

点分布の一様性すなわち最も効率の良い配置

などの特徴が表れている。

1/τ=(√5-1)/2=[0:1,1,1,1,・・・]=222.5

補角: 1/τ2=1-1/τ=(3-√5)/2=[0:2,1,1,1,・・・]=137.5

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

動径方向の分布則としてフェルマーらせんを仮定する

一様分布になるためにはフェルマーらせんに限ることが証明されている(r2=aθ, r=aθ1/2)

フェルマーらせんと黄金角が結びつくと、原点付近から無限遠まで一様な点分布が形成される

黄金角以外であっても、もし無限遠において一様分布を示すならば、フェルマーらせん上の点配置になっているのである。（原点付近での振る舞いについては予測困難）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝