ｘ軸に平行な直線（ｘ=β、ｙ＝R）を（ｎ−２）公転について１回自転させてみる．その際，公転と自転の向きを同方向にとると，

　　［Ｘ］＝［　ｃｏｓθ，-ｓｉｎθ］［ｘ］＋ａｃｏｓ（ｎ−２）θ

　　［Ｙ］＝［ｓｉｎθ，ｃｏｓθ］［ｙ］＋ａｓｉｎ（ｎ−２）θ

　その運動族

　　ｘ＝βｃｏｓ（θ）-Ｒsin（θ）＋ａｃｏｓ（（ｎ−２）θ）

　　ｙ＝βｓｉｎ（θ）+Ｒcos（θ）＋ａｓｉｎ（（ｎ−２）θ）

に対して

　　（∂ｙ／∂β）（∂ｘ／∂θ）−（∂ｘ／∂β）（∂ｙ／∂θ）＝０

を計算すると・・・

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

∂ｘ／∂β＝ｃｏｓ（θ）

∂ｙ／∂θ＝βcosθ-Ｒｓｉｎ（θ）＋(n-2)ａcos（（ｎ−２）θ）

∂y／∂β＝sin（θ）

∂x／∂θ＝-βsinθ-Ｒcos（θ）-(n-2)ａｓｉｎ（（ｎ−２）θ）

β=-(n-2)acos(n-3)θ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　　ｘ＝βｃｏｓ（θ）-Ｒsin（θ）＋ａｃｏｓ（（ｎ−２）θ）

　　ｙ＝βｓｉｎ（θ）+Ｒcos（θ）＋ａｓｉｎ（（ｎ−２）θ）

に代入すると

　　ｘ＝-(n-2)accos(n-3)θｃｏｓ（θ）-Ｒsin（θ）＋ａｃｏｓ（（ｎ−２）θ）

　　ｙ＝-(n-2)accos(n-3)θｓｉｎ（θ）+Ｒcos（θ）＋ａｓｉｎ（（ｎ−２）θ）

ｘ＝-(n-2)a/2{cos(n-2)θ+ｃｏｓ(n-4)θ）}-Ｒsin（θ）＋ａｃｏｓ（（ｎ−２）θ）

ｙ＝-(n-2)a/2{sin(n-2)θ-ｓｉｎ(n-4)θ}+Ｒcos（θ）＋ａｓｉｎ（（ｎ−２）θ）

２倍して整理すると

ｘ＝-(n-2)a{cos(n-2)θ+ｃｏｓ(n-4)θ）}-2Ｒsin（θ）＋2ａｃｏｓ（（ｎ−２）θ）

ｙ＝-(n-2)a{sin(n-2)θ-ｓｉｎ(n-4)θ}+2Ｒcos（θ）＋2ａｓｉｎ（（ｎ−２）θ）

x=-(n-4)acos(n-2)θ-(n-2)acos(n-4)θ-2Rsinθ

y=-(n-4)asin(n-2)θ+(n-2)asin(n-4)θ+2Rcosθ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
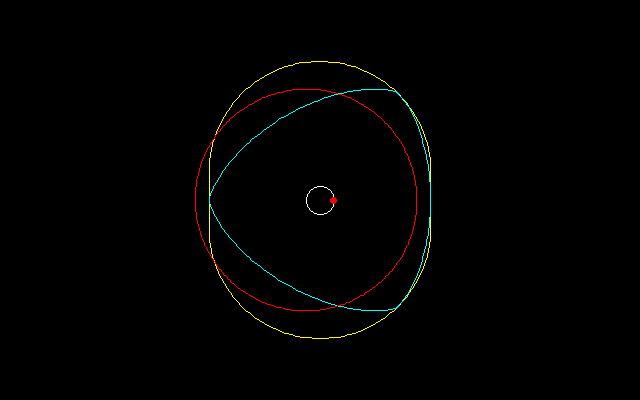