【３】接線極座標と内転形

　卵形線上に原点をとり，曲線上の点Ｐ（ｘ0，ｙ0）における接線とｘ軸とのなす角度をθとすると，

接線方向の単位ベクトル　　：　ｅ1＝（ｃｏｓθ，ｓｉｎθ）

それと直交する単位ベクトル：　ｅ2＝（−ｓｉｎθ，ｃｏｓθ）

となります．

　また，接線の方程式は

　　ｙ−ｙ0＝ｔａｎθ（ｘ−ｘ0）

　　（ｘ−ｘ0）ｓｉｎθ−（ｙ−ｙ0）ｃｏｓθ＝０

　　ｘｓｉｎθ−ｙｃｏｓθ＝ｘ0ｓｉｎθ−ｙ0ｃｏｓθ＝ｐ（θ）

と表されます．このとき，右辺はベクトルＰＯと法線ベクトルの内積ですから，原点から接線までの距離は｜ｐ（θ）｜で与えられます．

　すなわち，曲線上の点Ｐにおける接線に原点Ｏから引いた垂線の長さをｐ，接線とｘ軸とのなす角度をθとすると，

　　ｘｓｉｎθ−ｙｃｏｓθ＝ｐ（θ）

と表されます．（ｐ，θ）を接線極座標といいます．

　アステロイドの平行曲線の接線極座標は

　　ｘ＝ａｃｏｓ^3θ＋ｒｓｉｎθ

　　ｙ＝−ａｓｉｎ^3θ−ｒｃｏｓθ

を代入して

　　ｐ（θ）＝ａｓｉｎ２θ／２＋ｒ

で与えられます．

　ここで，ω＝２π／３とおくと，

　　ｐ（θ）＋ｐ（θ＋ω）＋ｐ（θ＋２ω）＝３ｒ＝ｈ（一定）

ですから，内転形であるための条件を満たします．

　また，その曲率半径は

　　ρ（θ）＝ｐ（θ）＋ｐ”（θ）

　＝ａｓｉｎ２θ／２＋ｒ−２ａｓｉｎ２θ＝ｒ−３／２ａｓｉｎ２θ≧０

より，ｒ≧３／２ａに対し，アステロイドの平行曲線

　　ｘ＝ａｃｏｓ^3θ＋ｒｓｉｎθ

　　ｙ＝−ａｓｉｎ^3θ−ｒｃｏｓθ

は特異点をもたずに高さｈ＝３ｒの正三角形に内接しながら回転することができる図形であることがわかります．

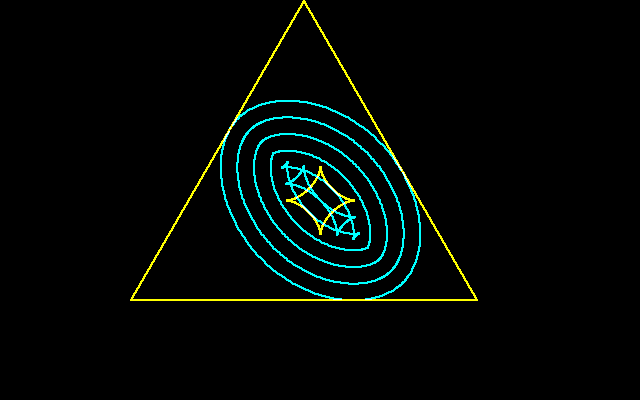
　ａ＝１，ｒ＝３の場合を図示すると

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝