黄色の線で示したペリトロコイド

　　ｘ＝（Ｒ−ｒ）ｃｏｓθ＋Ｒｃｏｓ（（Ｒ−ｒ）/Ｒθ）

　　ｙ＝（Ｒ−ｒ）ｓｉｎθ−Ｒｓｉｎ（（Ｒ−ｒ）/Ｒθ）

では、長さ２Ｒの線分を１回転させることができる。(尖点が奇数の場合）

　そこで、掛谷の定数のような面積の極限値を求めてみたい。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

[1]R=2r

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

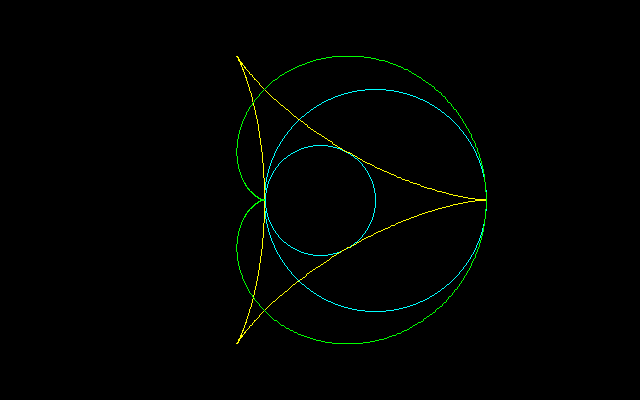
[2]R=3r

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

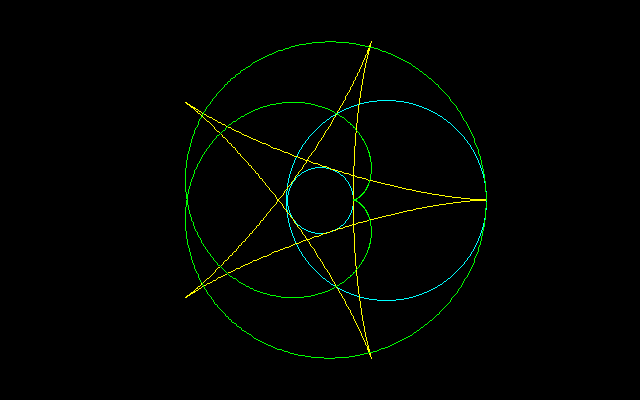
[3]R=4r

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

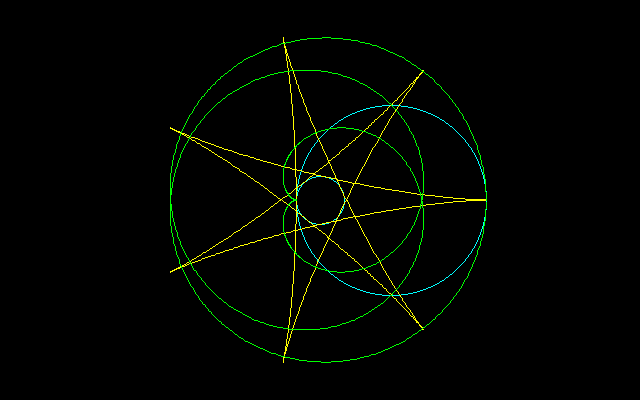
[4]R=5r

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
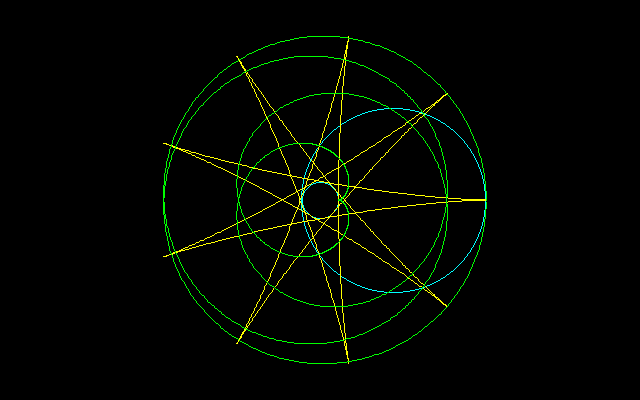