複素変数ｚの関数

　ｆ（ｚ）＝ｚ^3-６ｚ^2＋９ｚ-４＝０

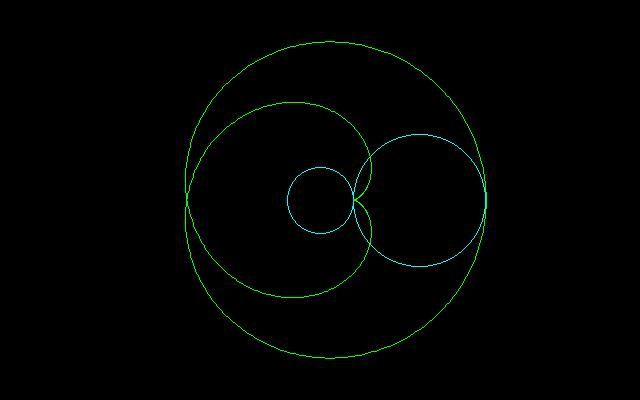
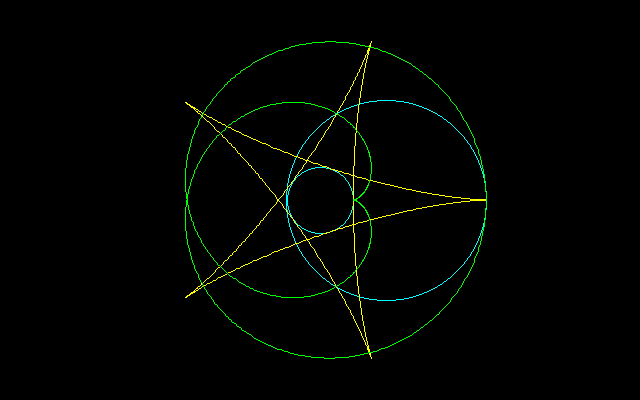
において、ｚは複素平面上に（その１）に掲げたような回転経路を描く。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

そのような数はすべて｜ｚ｜≦８を満たす。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

（その３）より、円板｜ｚ｜≦８のなかには少なくとも根ｚが存在する。

ｆはｚの連続関数だから、ωはｔによって連続的に決まる整数値の関数である。連続な整数値関数は定数しかないから、

｜ｚ｜≦８に根が存在しなければωは定数である。ところがこれはωが０と３の2つの値をとるという事実に矛盾する。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝