複素変数ｚの関数

　ｆ（ｚ）＝ｚ^3-６ｚ^2＋９ｚ-４＝０

において、ｚは複素平面上に（その１）に掲げたような回転経路を描く。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

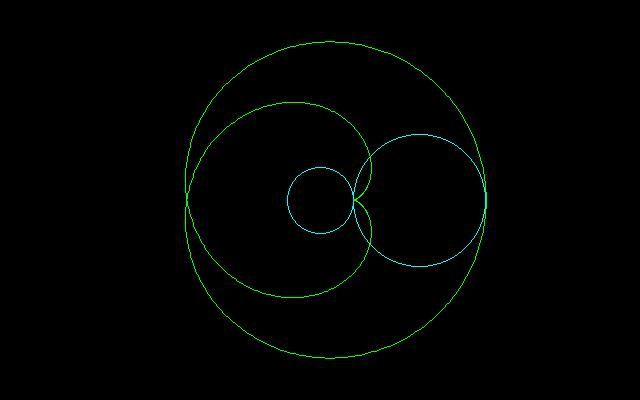
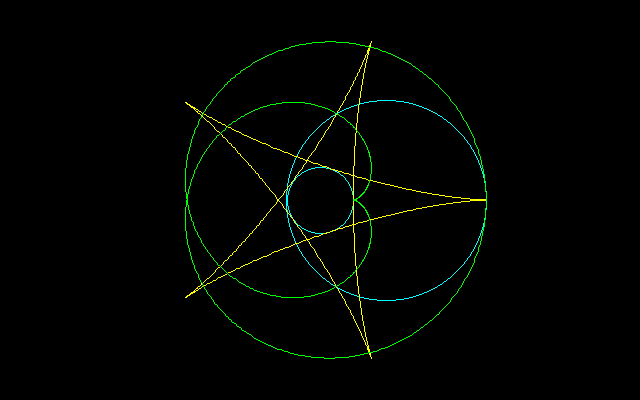
ｚが原点を中心とした半径ｔ≧０の円上を反時計回りに動くとき、複素平面上に描く経路を考える。

この円の内部のすべての複素数ｚに対してｆ（ｚ）≠０であれば、ｆの回転数ω＝ω（ｔ）をこの経路が原点の周りをまわっている回数として定義することができる。

ωは原点とｆ（ｚ）を結ぶ直線が掃く角度を表していて、２πの倍数になる。

半径ｔ＝０なら円は原点となり原点の像ｆ（０）は定数-４であるから、この経路は原点の周りをまわらない。ω（０）＝０

ｔ＞８とすると｜ｆ（ｚ）-ｚ^3｜＝｜-６ｚ^2＋９ｚ-４｜≦６｜ｚ｜^2＋９｜ｚ｜＋４が成り立つが、

これはｔ^2（６＋９/ｔ＋４/ｔ^2）＜8ｔ^2＜ｔ^3＝｜０−ｚ^3｜

したがって、｜ｆ（ｚ）-ｚ^3｜＜｜０−ｚ^3｜原点からｚ^3までの距離より小さい。

→これらの回転数は等しく、ｚ^3の回転数は３なので、ｔ＞８ではω（ｔ）＝３

→|ｚ｜＞８ではｆ（ｚ）≠０を意味する。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝