以下の図のような骨組みをスケルトンと呼ぶことにする。

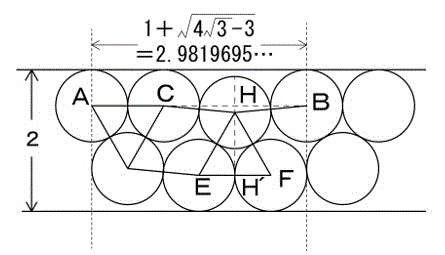
ここでは

　　[参]フランクル・前原「幾何学の散歩道」共立出版

にあるもうひとつのスケルトンで周期を算出して、個数を計算してみたい。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

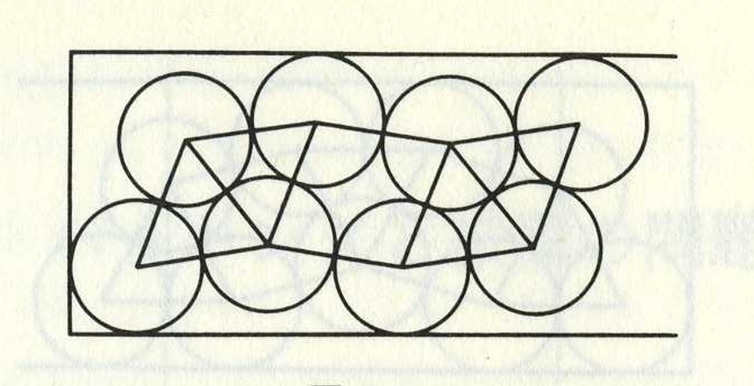
周期は円1と円5を比較すると

2√2+2/√3=3.98313

1周期内の4個の円が詰まるから、全部で約

4・2000/(2√2+2/√3)=2008.47個の円が詰まることになる

しかし、右端の円がはみ出るかもしれないので、

501・(2√2+2/√3)=1995.55<1998

502・(2√2+2/√3)=1999.53>1998

左端の半円と501組目までは入るが、502組目の一部分はみ出ることが分かる。

1+1995.55+√2-1/√3=1997.38

1+1995.55+√2+1/√3=1998.54

1+1995.55+2√2=1999.38→はみ出る

501・4+3＝2007個入る。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝