直径１の円を2×１０００の長方形の中に詰め込む問題を考える。

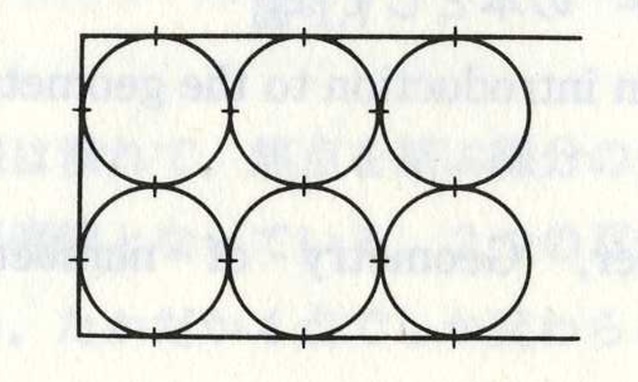
この問題はグラハムが講演で紹介したものであるという（グラハムのパッキング）。正方格子状配置では2000枚、三角格子状配置では1999枚詰め込むことができるが、後者では円1枚分の隙間を生じてしまうというわけである。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　そこで、三角形配置の次に逆三角形配置を交互に並べた以下のような配置を考えると、2011枚はいることが計算される。

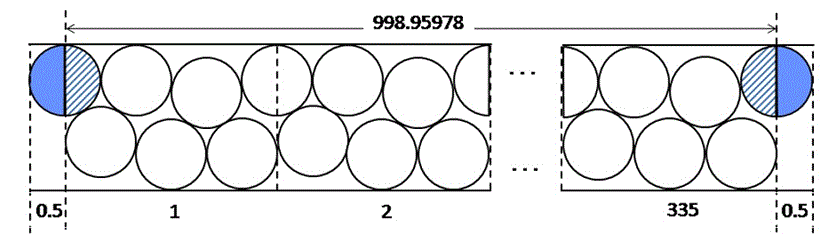
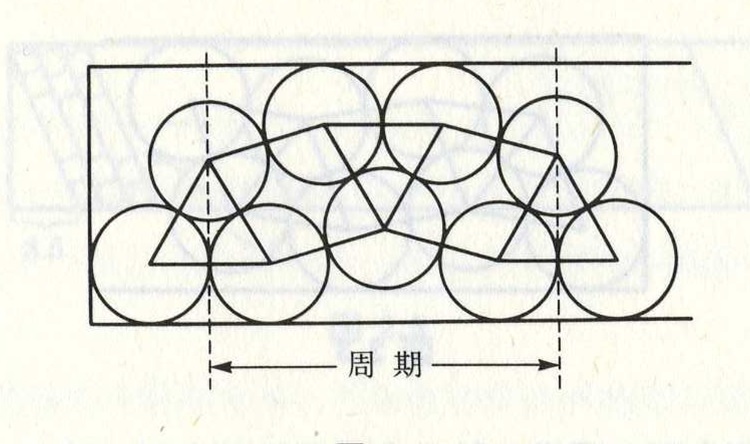
すなわち、2×１０００の長方形の中に直径１の円をはなくても2011枚詰め込むことができることがわかった。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝