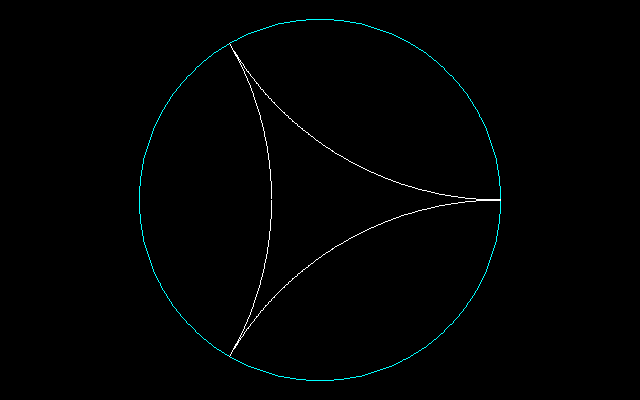包絡線星状図形の面積は5分枝で（面積0.448431）

11分枝（面積0.391406）で、デルトイドより小さくなる。

分枝の数が多くなるほど面積は徐々に小さくなるように思える。

しかし、実際に計算してみると25分枝までは減少するのだが、その後徐々に増加していく

最小面積は0.3846くらいかと思われる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　それに対して、円弧星状図形の分枝の数を増すと、その面積はゆっくりながら減少していき、その値は

掛谷の定数 0.284258224・・・

に限りなく近づく。

これが現在知られている最良の値である。はたして、この値より小さい値を実現できるであろうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

[１]（面積0.396782）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

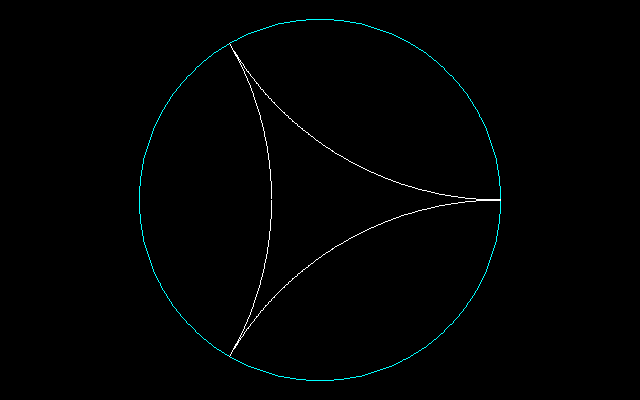
[２]（面積0.316801）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

[３]（面積0.300015）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

[４]（面積0.293596）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝