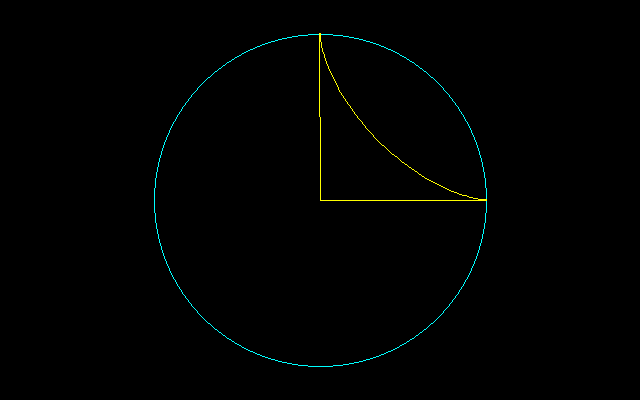長さ1の線分の両端点がそれぞれｘ軸、ｙ軸上にあるとき、その包絡線を求める。

線分の方程式は

x/cosθ+y/sinθ=1

包絡線を求めるにはまずθで偏微分して

x・sinθ/(cosθ)^2-y・cosθ/(sinθ)^2=0

連立方程式を解くと、xについて

　　x=(cosθ)^3

yについて、

　　y=(sinθ)^3

これはアステロイドである。以下の場合はどうだろう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

[１]アステロイド

アステロイドの第1象限は針を９０°回転させることができる。

同じものを2つ貼り合わせると完全に1回転させることができる。

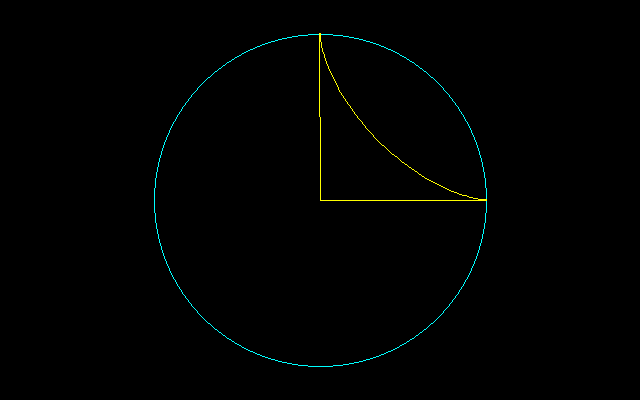
[２]

１２０°で交わる2つの直線上で、針の両端を滑らせることによって得られる図形は針を６０°回転させることができる。

この図形を3つ貼り合わせると５尖点図形が出来上がるが、この図形は完全に1回転させることができる。

[３]

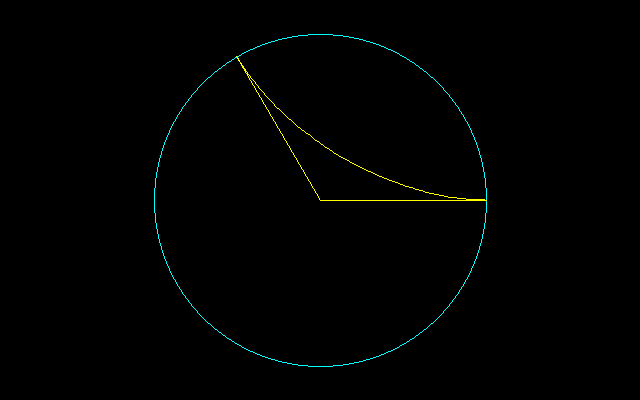
１３５°で交わる2つの直線上で、針の両端を滑らせることによって得られる図形は針を４５°回転させることができる。

この図形を4つ貼り合わせると7尖点図形が出来上がるが、この図形は完全に1回転させることができる。

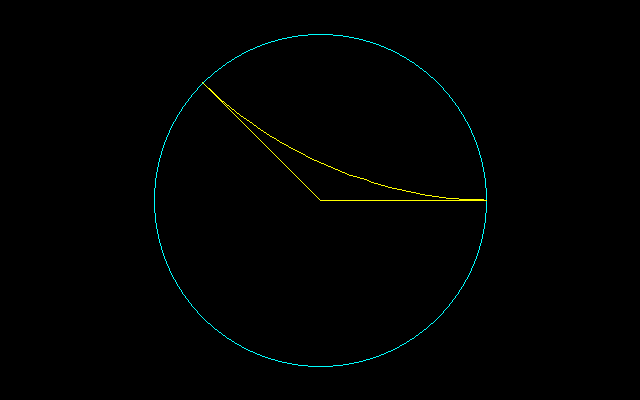
[４]

１４４°で交わる2つの直線上で、針の両端を滑らせることによって得られる図形は針を３６°回転させることができる。

この図形を5つ貼り合わせると９尖点図形が出来上がるが、この図形は完全に1回転させることができる。

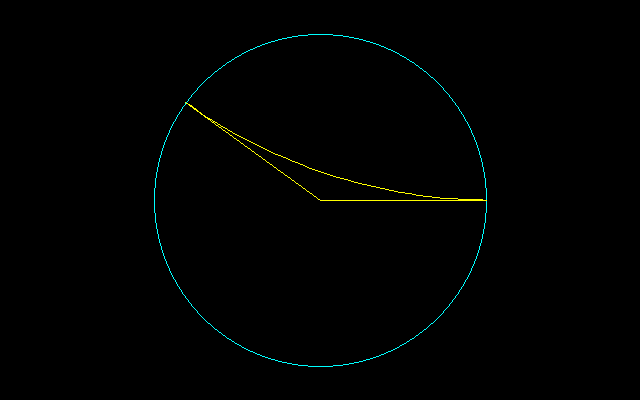
[５]

１５０°で交わる2つの直線上で、針の両端を滑らせることによって得られる図形は針を３０°回転させることができる。

この図形を6つ貼り合わせると１１尖点図形が出来上がるが、この図形は完全に1回転させることができる。

この図形の面積は0.39140で、デルトイドより小さい。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

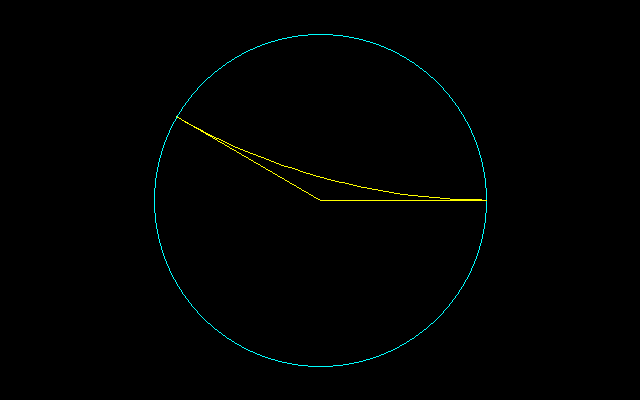
１８０-１８０/ｎ°で交わる2つの直線上で、針の両端を滑らせることによって得られる図形は針を１８０/ｎ°回転させることができる。

この図形をｎ個貼り合わせると２ｎ-1尖点図形が出来上がるが、この図形は完全に1回転させることができる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝