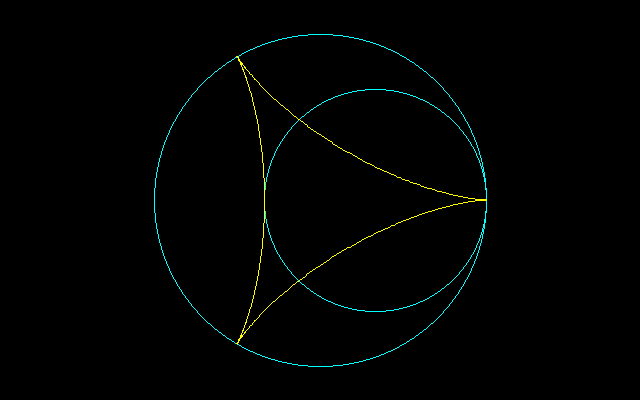ｘ＝（Ｒ−ｒ）ｃｏｓθ＋Ｒｃｏｓ（+/-（Ｒ−ｒ）/Ｒθ）

　　ｙ＝（Ｒ−ｒ）ｓｉｎθ−Ｒｓｉｎ（+/-（Ｒ−ｒ）/Ｒθ）

星状図形はハイポサイクロイドとしても描くことができるが、掛谷の問題を考えるにあたっては、ペリトロコイドのほうが便利である。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

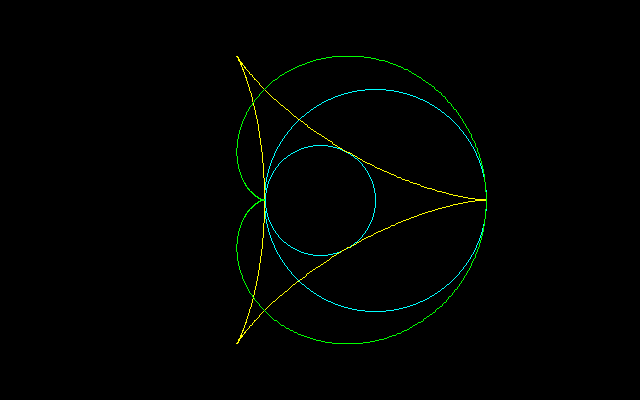
[1]R=2r

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

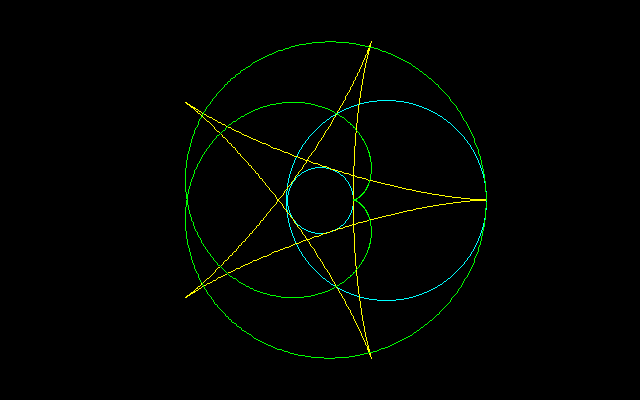
[2]R=3r

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

[3]R=4r

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

[4]R=5r

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝