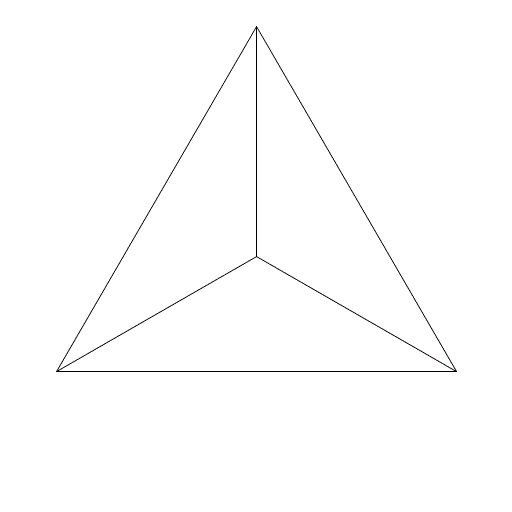
ｎ次元立方体の頂点配置から互い違いに頂点を取ることで、半立方体を作成することができます。

　ｎ＝３の場合は正四面体、ｎ＝４の場合は正１６胞体になりますが、n＞４では２種類のファセットで構成された一種の準正多胞体になります。

　４次元立方体の１６頂点（±１、±１、±１、±１）から偶数頂点のみをとると

　　±（１，１，１，１）

　　±（１，１，−１，−１）

　　±（１，−１，１，−１）

　　±（１，−１，−１，１）

の８頂点になりますが、ベクトル

　　（１，１，１，１）

　　（１，１，−１，−１）

　　（１，−１，１，−１）

　　（１，−１，−１，１）

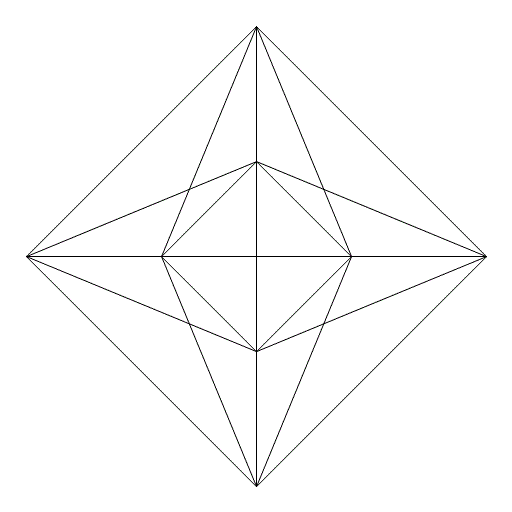
が互いに直交し、その長さがすべて２で等しいことから正１６細胞体をなすことが分かります。

　しかし、投影する方向によっては本当に正１６胞体なのかどうかわかりにくくなってしまいます。ｎ＝３の場合とｎ＝４の場合を掲げます。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝