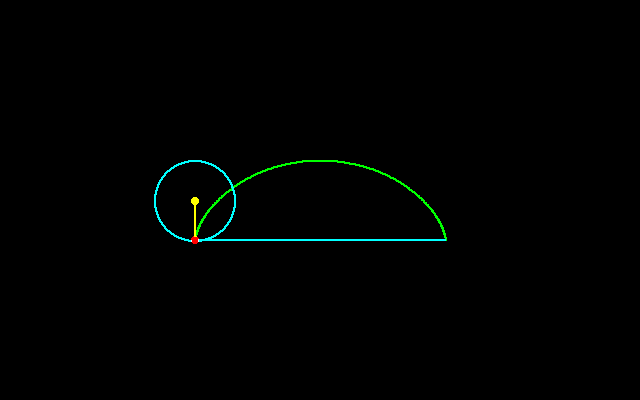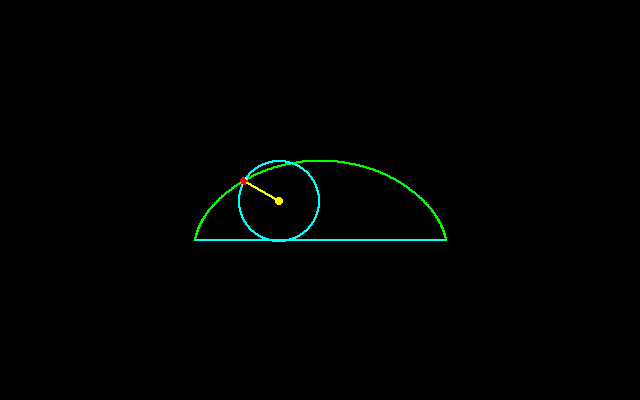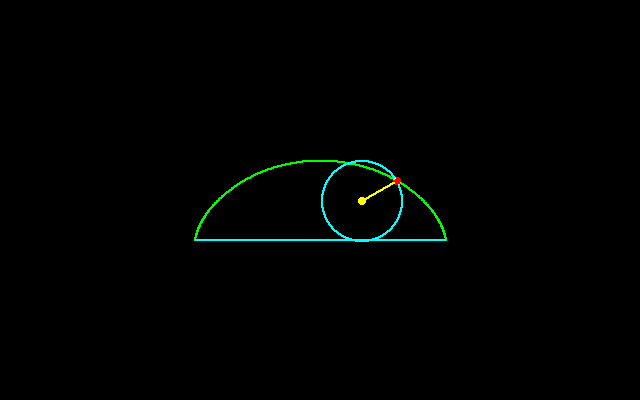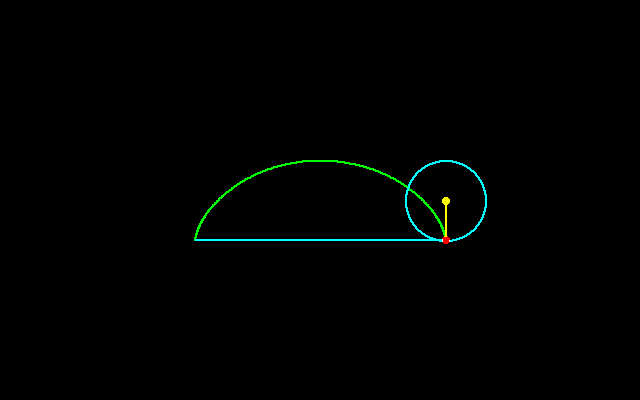
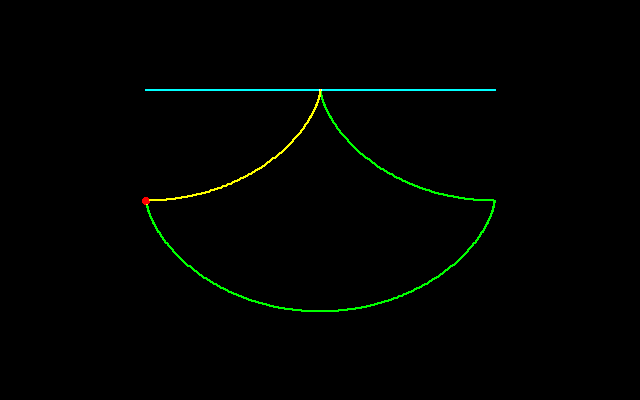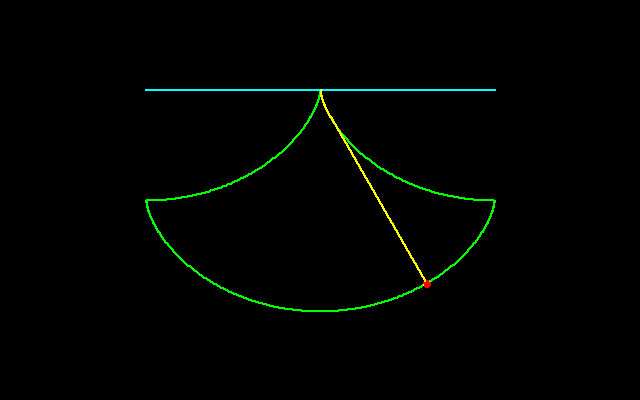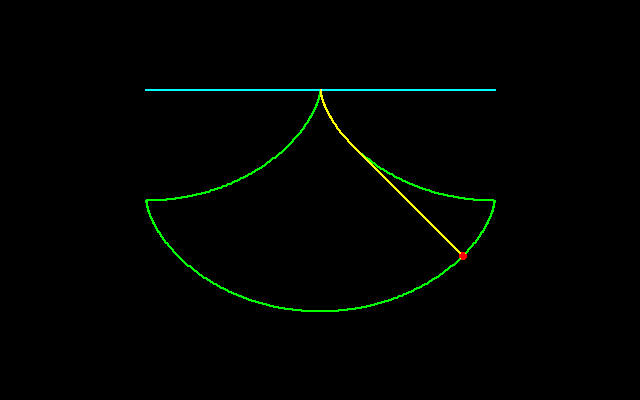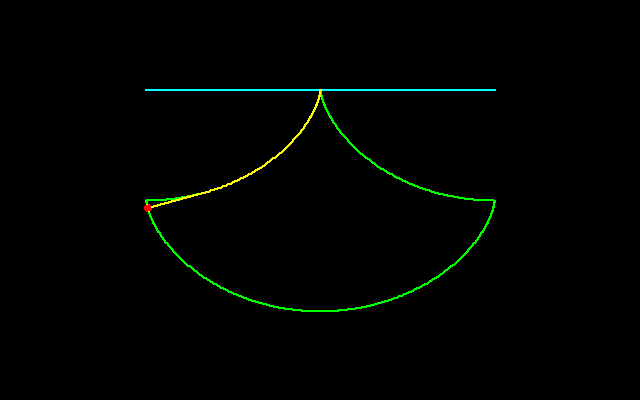
サイクロイドは転がる円の円周上の点の軌跡である．

　ガリレオはサイクロイドの下側の面積と円の面積はどのような関係にあるのかと考え，トリチェリとともに，円の面積はサイクロイドの面積のちょうど１／３であることつきとめた．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［補］サイクロイド曲線の長さは円の直径の４倍，しなわち，円の外接正方形の周長に等しい．

［補］長方形に内接する放物線を描いて，放物線の面積が長方形の面積の２／３であることをつきとめたのはアルキメデスである．放物線をその軸を中心に加点させるとコノイドができる．コノイドの体積もまた外接する円筒の２／３になる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝