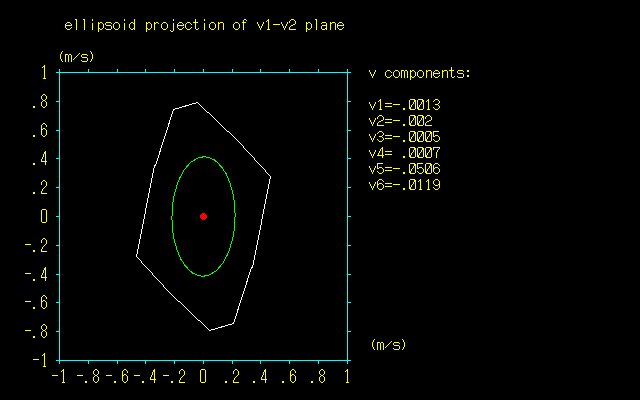
（その２）では６次元直方体の投影図を描いたが，予想通り，稜線はかなり混み入っていた．すべての稜線をそのまま表示する方法では，ｎ次元直方体はかえって理解しにくくなる．

　

　稜線のうち，ロボティクス的に最も重要なものは輪郭線である．そこで，今回のコラムでは，２次元平面に投影した際の混雑した稜線の中から，輪郭線だけを抽出することを試みた．

　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　

　ところで，３次元の立体図形を平面上に描写する際，裏側のみえない図形で隠れた線が表示されていると大変見にくくなる．そこで，陰になる部分を消して立体感や遠近感を深めるという問題が生ずる．これを陰線処理というのだが，図形の裏側を消去するのが隠線処理，図形の内部を消去するのが輪郭線処理で，これらは同源同根の問題であって，いずれも「計算機科学」の分野に入る．

　

　ここまで読み進んでこられた読者にとってはすでにご存知のことかと思われるが，一般的な図形を２次元平面上に投影した際にできる輪郭線を描く手順は以下の通りである．

　

（１）ｎ個の頂点の座標を求める（その２にて既述）

（２）それを平面に投影した際の凸包を求める

　

　平らな板の上に，同一直線上にないｎ個の点をとり，そこに釘を打つ．この釘に輪ゴムをかけると，ｎ個の中のいくつかを頂点とする凸多角形が得られる．この凸多角形が凸包である．しかし，（馬鹿正直に）凸包を求めようとするとかなりの時間のかかることが予測されるし，このような「計算機科学」的隠線処理の方法が３次元の枠組みを超えたのは最近の事なので，求めているｎ次元図形の隠線処理・輪郭線処理が一般化・体系化されているかどうかはわからない．

　

　そこで，本稿ではｎ次元立方体という図形の特徴を活かした輪郭線処理を取り上げたいと思う．ｎ次元立方体を図に描く場合，凸包を求める方法に比べて，格段といいアルゴリズムが存在するのである．

　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　

　陰線処理にはいくつかの方法があげられる．

　

１．描画の順序による消去法

　画面上の図形は次に描く図形によって重なる部分が消去されるから，ｚ軸の負の方向（奥行きで視点から遠い方）から，各面を輪郭描画と別色での塗りつぶしを行う方法である．塗りつぶしはディスプレイの特長を利用した消去法といえるであろう．

　

２．計算によって隠れる部分を表示しない方法

　原点を中心とした球や多面体などの３次元図形が直角座標内に正射影で描かれている場合には，物体の各面に原点より下した垂線の足の座標（ｘ，ｙ，ｚ）を求め，ｚの値が負のときはみえない部分であると判定できる．この方法は，たとえば，経線・緯線の入った球面を描写するなど，図形によっては比較的簡単に計算できる．

　

３．最大値・最小値法

　最大値，最小値を配列に読み込んでおき，それと表示しようとする点の位置を比較することによって隠線処理する方法である．最大値より大きい場合と最小値より小さい場合だけを表示するようにすれば，隠れた部分を表示しないで済む．ただし，この方法では比較回数が多くなるため，実行時間が長くなるという欠点がある．

　

　ここで採用したｎ次元立方体の輪郭線処理は，３次元立方体はもちろん，一般次元の立方体にも対応した消去プログラムである．２と３を折衷した方法ともいえるのだが，その考え方と手順を列記しておく．

　

ａ）ｎ次元立方体（正２ｎ胞体）では，各頂点のまわりにはｎ本の稜，ｎ（ｎ−１）／２本の正方形が集まっている．また，各稜のまわりにはｎ−１個の正方形が集まっている．

　

ｂ）１つの稜のまわりの正方形面上で，いま描こうとしている稜に平行なｎ−１本の線を求める（5030〜5150行）．

　

ｃ）これらｎ本の平行線をそれぞれ２次元平面に投影した際の直線を含む３次元空間内の平面の，稜の始点（あるいは終点）におけるｚ値を求める（5170〜5200行）．

　

ｄ）ｎ本の線のなかで，稜のｚ値が最大値，最小値の場合だけを表示するようにすれば，輪郭線だけを表示することができる（5220〜5330行）．

　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　

　

4640 '

4650 ' *** 超直方体 ***

4660 '

4670 *HYPERCUBE:

4680 T=1:' [non-stochastic]

4690 FOR IS=1 TO M:EDGE(IS)=SQR(T*AZ(IS,IS)):NEXT IS

4700 '

4710 FOR IS=0 TO 2^M-1

4720　 FOR JS=1 TO M:S(JS)=-1:NEXT JS

4730　 FOR JS=1 TO M

4740　　 IF (IS AND 2^(JS-1))=0 THEN S(JS)=1

4750　 NEXT JS

4760　'GOSUB *VERTEX:GXS=GX:GYS=GY

4770　 '

4780　 FOR JS=1 TO M:S0(JS)=S(JS):NEXT JS

4790　 FOR JS=1 TO M

4800　　'FOR KS=1 TO M:S(KS)=S0(KS):NEXT KS

4810　　'S(JS)=-S(JS)

4820　　'GOSUB *VERTEX:GXE=GX:GYE=GY

4830　　'LINE(GXS,-GYS)-(GXE,-GYE),7

4840　　 GOSUB *POLYGON.LINE

4850　 NEXT JS

4860 NEXT IS

4870 RETURN

4880 '

4890 ' *** 頂点 ***

4900 '

4910 *VERTEX:

4920 GX=0:GY=0

4930 FOR LS=1 TO M

4940　 GX=GX+BZ(I,LS)*EDGE(LS)*S(LS)

4950　 GY=GY+BZ(J,LS)*EDGE(LS)*S(LS)

4960 NEXT LS

4970 GX=GX+VO(I):GY=GY+VO(J)

4980 RETURN

4990 '

5000 ' *** 輪郭抽出 ***

5010 '

5020 *POLYGON.LINE:

5030 EPS=.05

5040 FOR KS=1 TO M

5050　 FOR LS=1 TO M:S(LS)=S0(LS):NEXT LS

5060　 IF KS=JS THEN 5080

5070　 S(KS)=S(KS)*(1-EPS)

5080　 GOSUB *VERTEX:GXS(KS)=GX:GYS(KS)=GY

5090　 '

5100　 FOR LS=1 TO M:S(LS)=S0(LS):NEXT LS

5110　 S(JS)=-S(JS)

5120　 IF KS=JS THEN 5140

5130　 S(KS)=S(KS)*(1-EPS)

5140　 GOSUB *VERTEX:GXE(KS)=GX:GYE(KS)=GY

5150 NEXT KS

5160 '

5170 X=GXS(JS):Y=GYS(JS)

5180 FOR KS=1 TO M

5190　 GZ(KS)=(GYE(KS)-GYS(KS))*(X-GXS(KS))-(GXE(KS)-GXS(KS))*(Y-GYS(KS))

5200 NEXT KS

5210 '

5220 ZMAX=GZ(JS):ZMIN=GZ(JS)

5230 FOR KS=1 TO M

5240　 IF KS=JS THEN 5270

5250　 IF ZMAX<GZ(KS) THEN ZMAX=GZ(KS)

5260　 IF ZMIN>GZ(KS) THEN ZMIN=GZ(KS)

5270 NEXT KS

5280 '

5290 SW=0

5300 IF (ZMAX-GZ(JS))*(ZMIN-GZ(JS))=0 THEN SW=1

5310 GXS=GXS(JS):GYS=GYS(JS)

5320 GXE=GXE(JS):GYE=GYE(JS)

5330 IF SW=1 THEN LINE(GXS,-GYS)-(GXE,-GYE),7

5340 RETURN

　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　

【余白】

　

　最後に，ｎ次元ではなく，３次元の問題も取り上げておきたい．とはいってもまったく架空の問題ではなく，分子動力学の計算に際して，実際に提出された基本的な問題である．

　

　聞くところによると，某大学の計算機科学の教授が解けなかった問題で，そのため小生のところにたどりついたということらしい．高校生でも解ける問題と思うのだが，・・・．

　

　解答はプログラムの形で与えておくが，［２］では分母が０のときの対策が必要になることを申し添えておきたい．

　

［１］点A(a1,a2,a3),B(b1,b2,b3),C(c1,c2,c3)がある．面ABC上にあって，線分ABに垂直で，C側にある点で，ABと同じ長さの線分APの点P(p1,p2,p3)を求めよ．

　

（例）

A(1,0,0),B(3,0,0),C(2,3,0)→P(1,2,0)

A(0,2,0),B(3,2,0),C(2,0,0)→P(0,-1,0)

A(1,0,2),B(3,0,2),C(4,0,5)→P(1,0,4)

A(-1,1,1),B(1,1,1),C(2,1,5)→P(-1,1,3)

　

1000 '

1010 ' *** molecular dynamics ***

1020 '　　　　　　　 2002/10/23 (C) ｻﾄｳ ｲｸﾛｳ

1030 SCREEN 3,0:CONSOLE ,,0,1

1040 WIDTH 80,25:COLOR 6

1050 CLS 3

1060 M=3:N=4

1070 DIM X(M),Y(M),Z(M)

1080 '

1090 FOR J=1 TO N

1100　 GOSUB *CALC

1110 NEXT J

1120 END

1130 '

1140 *CALC:

1150 FOR I=1 TO M

1160 READ X(I),Y(I),Z(I)

1170 NEXT I

1180 '

1190 N1=X(2)-X(1)

1200 N2=Y(2)-Y(1)

1210 N3=Z(2)-Z(1)

1220 O1=X(3)-X(1)

1230 O2=Y(3)-Y(1)

1240 O3=Z(3)-Z(1)

1250 '

1260 R1=N1*N1+N2*N2+N3*N3

1270 R2=N1*O1+N2*O2+N3*O3

1280 K=-R1/R2

1290 '

1300 Q1=N1+O1*K

1310 Q2=N2+O2*K

1320 Q3=N3+O3*K

1330 R3=Q1*Q1+Q2*Q2+Q3*Q3

1340 S=SQR(R1/R3)

1350 GOSUB *CALC.SUB

1360 RR=O1*X1+O2*X2+O3*X3

1370 IF RR<0 THEN S=-S:GOSUB *CALC.SUB

1380 '

1390 P1=X1+X(1)

1400 P2=X2+Y(1)

1410 P3=X3+Z(1)

1420 PRINT

1430 PRINT "p1=";P1

1440 PRINT "p2=";P2

1450 PRINT "p3=";P3

1460 RETURN

1470 '

1480 *CALC.SUB:

1490 T=S*K

1500 X1=N1*S+O1*T

1510 X2=N2*S+O2*T

1520 X3=N3*S+O3*T

1530 RETURN

1540 '

1550 DATA 1,0,0

1560 DATA 3,0,0

1570 DATA 2,3,0

1580 '

1590 DATA 0,2,0

1600 DATA 3,2,0

1610 DATA 2,0,0

1620 '

1630 DATA 1,0,2

1640 DATA 3,0,2

1650 DATA 4,0,5

1660 '

1670 DATA -1,1,1

1680 DATA 1,1,1

1690 DATA 2,1,5

　

［２］点A(a1,a2,a3),B(b1,b2,b3),C(c1,c2,c3)がある．面ABCに垂直で，線分ABを含む面上にあって，線分ABに垂直で，ABと同じ長さの線分APの点P(p1,p2,p3)を求めよ．

　

1000 '

1010 ' *** molecular dynamics ***

1020 '　　　　　　　 2002/10/23 (C) ｻﾄｳ ｲｸﾛｳ

1030 SCREEN 3,0:CONSOLE ,,0,1

1040 WIDTH 80,25:COLOR 6

1050 CLS 3

1060 M=3:N=4

1070 DIM X(M),Y(M),Z(M)

1080 '

1090 FOR J=1 TO N

1100　 GOSUB *CALC

1110 NEXT J

1120 END

1130 '

1140 *CALC:

1150 FOR I=1 TO M

1160 READ X(I),Y(I),Z(I)

1170 NEXT I

1180 '

1190 N1=X(2)-X(1)

1200 N2=Y(2)-Y(1)

1210 N3=Z(2)-Z(1)

1220 O1=X(3)-X(1)

1230 O2=Y(3)-Y(1)

1240 O3=Z(3)-Z(1)

1250 '

1260 R1=N1*N1+N2*N2+N3*N3

1270 Q1=N2*O3-N3*O2

1280 Q2=N1*O3-N3*O1

1290 Q3=N2*O1-N1*O2

1300 R2=Q1*Q1+Q2*Q2+Q3*Q3

1310 '

1320 IF Q1<>0 THEN GOSUB *Q1:GOTO 1350

1330 IF Q2<>0 THEN GOSUB *Q2:GOTO 1350

1340 GOSUB *Q3

1350 '

1360 RETURN

1370 '

1380 *CALC.SUB:

1390 P1=K1+X(1)

1400 P2=K2+Y(1)

1410 P3=K3+Z(1)

1420 PRINT

1425 PRINT "data=";J

1430 PRINT "p1=";P1

1440 PRINT "p2=";P2

1450 PRINT "p3=";P3

1460 RETURN

1470 '

1480 *Q1:

1490 K1=SQR(Q1*Q1*R1/R2)

1500 K2=-Q2/Q1*K1

1510 K3=-Q3/Q1*K1

1520 GOSUB *CALC.SUB

1530 K1=-K1:K2=-K2:K3=-K3:GOSUB *CALC.SUB

1540 RETURN

1550 '

1560 *Q2:

1570 K2=SQR(Q2*Q2*R1/R2)

1580 K1=-Q1/Q2*K2

1590 K3= Q3/Q2*K2

1600 GOSUB *CALC.SUB

1610 K1=-K1:K2=-K2:K3=-K3:GOSUB *CALC.SUB

1620 RETURN

1630 '

1640 *Q3:

1650 K3=SQR(Q3*Q3*R1/R2)

1660 K1=-Q1/Q3*K3

1670 K2= Q2/Q3*K3

1680 GOSUB *CALC.SUB

1690 K1=-K1:K2=-K2:K3=-K3:GOSUB *CALC.SUB

1700 RETURN

1710 '

1720 DATA 1,0,0

1730 DATA 3,0,0

1740 DATA 2,3,0

1750 '

1760 DATA 0,2,0

1770 DATA 3,2,0

1780 DATA 2,0,0

1790 '

1800 DATA 1,0,2

1810 DATA 3,0,2

1820 DATA 4,0,5

1830 '

1840 DATA -1,1,1

1850 DATA 1,1,1

1860 DATA 2,1,5

　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝