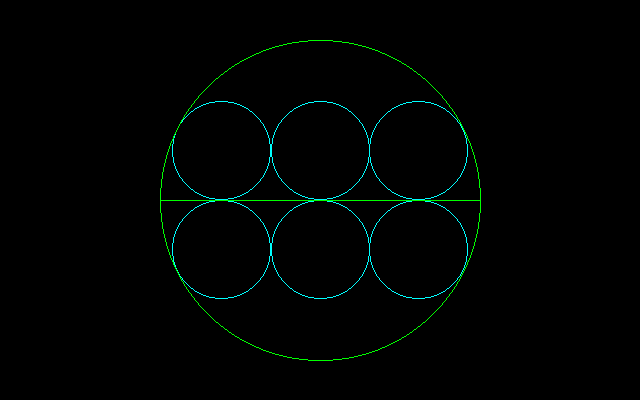
真田六文銭似の問題．下図において，大円の半径と小円の直径の比は黄金分割になっている．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　半径１の単位円の半円を考える．直径上に接点をもつ円（半径ｒ）を３個を内接させる．３円の中心は

　　Ａ（−２ｒ，ｒ）

　　Ｂ（０，ｒ）

　　Ｃ（２ｒ，ｒ）

　　ｒ√５＋ｒ＝１

　　ｒ＝１／（１＋√５）

　したがって，大きい半円の半径を小さい円の直径で割ると

　　１／２ｒ＝（１＋√５）／２＝φ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

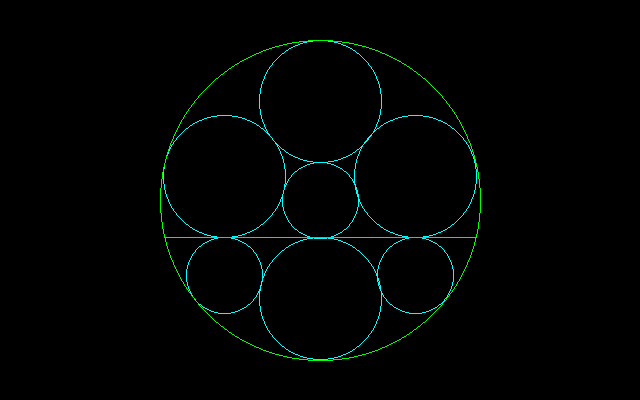
　下図において，中円と小円の大きさの比は黄金分割になっている．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　大円の半径を１とすると，

　中円の半径は（３−√５）／２，小円の半径は√５−２．

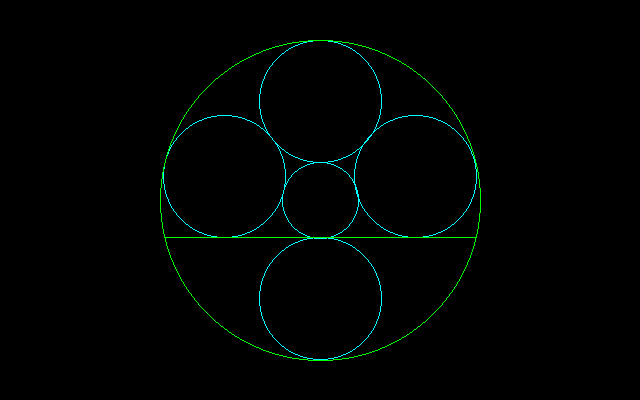
　ピタゴラスの定理だけで解けるので各自確かめられたい．また，この問題から２円を除いても解けるだろう．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝