（その３３）に掲げた下図は，黄金分割の別法になっている．

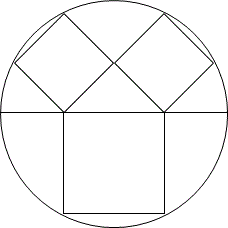
　この問題は大正方形の頂点上に小正方形が載っている図形の外接円に関する問題で，小正方形の頂点と大正方形の頂点が，同じ長さの半径からなる円上に存在するというものであった．この問題も３次元以上に拡張できるだろうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　ｎ次元立方体の上面の頂点の座標を

　　（±１，±１，・・・，±１，１）

とする．稜の長さが２の立方体である．

　小立方体（稜の長さｃ）の頂点の座標を

　　（１，１，・・・，１，１）

　　（１，１，・・・，１，ｃ√ｎ＋１）

とすることはできるが，たとえば，他の頂点を

　　（１，１，・・・，０，ｈ＋１）

　　（１，０，・・・，１，ｈ＋１）

　　（０，１，・・・，１，ｈ＋１）

となるように配置させることはできない．

　３次元の場合でやってみるとわかるのであるが，立方体の射影が六角形になってうまく行かないのである．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝