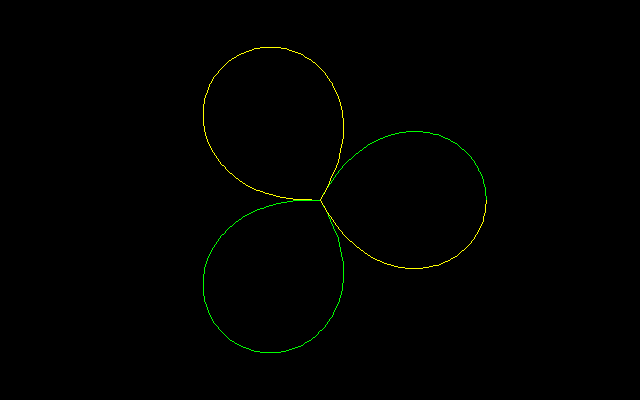
楕円は円を一方向に一定の倍率で伸縮したアフィン変換図形であるが,円のように弧長を2等分,3等分,5等分できなかった(その14).その意味では円のもつ性質を引きずっていないことになる.
それに対して,円もレムニスケートも2等分点,3等分点,5等分点もコンパスと定規を使って作図可能である.中間曲線は円とレムニスケートの中間にあることから私が勝手に名付けた曲線であるが,円のもつこの性質は中間曲線に遺伝しているだろうか? (その5)で行きあたりばったりの置換を行った結果では中間曲線の弧長を2等分することはできなかったのであるが,・・・
===================================
【1】着想
(その15)で,中間積分
I=∫dx/(1−x^3)^1/2
を考えたのだが,それは第1種楕円積分となることが示された.
ところで,第1種楕円積分の標準形
F(k,x)=∫(0,x)1/{(1-x^2)(1-k^2x^2)}^(1/2)f(x)dx
については加法公式
z={x(1+my^2+ny^4)^1/2+y(1+mx^2+nx^4)^1/2}/(1−nx^2y^2)
m=−(1+k^2),n=k^2
が使える.
そこで,中間積分に対応する半三つ葉型の中間曲線(12次曲線)
r^(3/2)=cos(3/2θ)
(2(x^2+y^2)^3−4x^3+3x(x^2+y^2))^2=(x^2+y^2)^3
のk等分点を求めてみようというのが今回のコラムの狙いである.
中間曲線のグラフは半三つ葉型(緑)であるが,以下の図には実の部分(緑)に加えて虚の部分(黄)も描いてある.
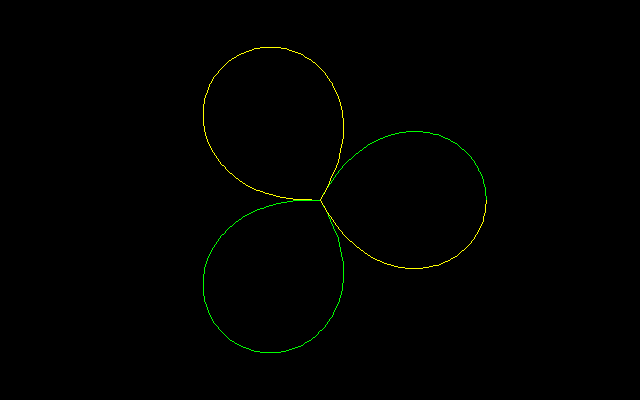
===================================
【2】第1種楕円積分の標準形への還元
積分
I=∫(c,1)dx/(1−x^3)^1/2
を考える.変換
y=(λx+μ)/(νx+ρ),x=(−ρy+μ)/(νy−λ)
を適当に選ぶことにより,常に
dy/(1+my^2+ny^4)^1/2
の形に還元できる.
λ=−1,μ=1−√3,ν=1,ρ=−1+√3
x=cに対するyの値を
y1=(c−1+√3)/(−c+1+√3)
とおくと
I=1/4√3∫(y1,1)2dy/((1−y^2)(2−√3+(2+√3)y^2)^1/2
ここで,y^2=1−z^2,z1^2=1−y1^2とおくと第1種楕円
I=1/4√3∫(0,z1)dz/((1−z^2)(1−k^2z^2)^1/2=1/4√3F(k,φ1)
となる.ただし,
k=(√2+√6)/4,k^2=(2+√3)/4
φ1=arccos((c−1+√3)/(−c+1+√3))=arcsin((1−y1^2)^1/2)
sinφ1=z1,z1=(1−y1^2)^1/2
c=1→z1=0
c=0→z1=(4√3−6)^1/2=α
これで,中間曲線の弧長を求める問題は,加法公式
z={x(1+my^2+ny^4)^1/2+y(1+mx^2+nx^4)^1/2}/(1−nx^2y^2)
m=−(1+k^2),n=k^2,α=(4√3−6)^1/2
の問題に還元されたことになる.
倍角公式
x’=2xy/(1−nx^4)=2x(1+mx^2+nx^4)^1/2/(1−nx^4)
より,2等分点に対応する楕円曲線上の点
2x(1+mx^2+nx^4)^1/2/(1−nx^4)=α
の解をx=βとすると,
1−((c−1+√3)/(−c+1+√3))^2=β^2
c=√3+1−2√3/((1−β^2)^1/2+1)
が中間曲線の2等分点である.
ここで注意しておきたいのはcは2等分点のx座標ではなく,極座標(r,θ)における動径rであるということである.レムニスケートの場合,
r^2=cos2θ=2cos^2θ−1=1/2sin^2θ
より,
cosθ=((1+r^2)/2)^1/2
sinθ=((1−r^2)/2)^1/2
したがって,
x=rcosθ=((r^2+r^4)/2)^1/2
y=rsinθ=((r^2−r^4)/2)^1/2
それに対して,中間曲線の場合は
r^(3/2)=cos(3/2θ)
3/2θ=arccos(r^3/2)
θ=2arccos(r^3/2)/3
x=rcosθ=rcos(2arccos(r^3/2)/3)
y=rsinθ=rsin(2arccos(r^3/2)/3)
となり解析的な条件下では解けないことになる.すなわち,加法公式は適用できても,k等分点は作図可能ではないのである.
===================================
【3】中間曲線のk等分点
阪本ひろむ氏にMathematicaで2等分点に対応する楕円曲線上の点
2x(1+mx^2+nx^4)^1/2/(1−nx^4)=α
を求めてもらったところ,メモリ不足のため,解析解は得られなかったが,数値解を計算することができた.(3等分点,5等分点はメモリ不足のため数値解すら計算できなかった.)
当初,中間曲線の場合も解析解が得られれば作図可能性に対する直接的な証明が可能となるのではと考えられたのであるが,たとえ解析解が得られたとしてもk等分点は作図可能ではないことが判明している.それでも数値的に2等分,4等分,8等分,・・・することは可能である.
2等分点,4等分点,8等分点に対応する楕円曲線上の点と中間曲線上の点の数値解は以下の如くである.
x c (x,y)
n=2 → 0.732051 → 0.671618 → (0.531137,0.411053)
n=4 → 0.43211 → 0.910585 → (0.856873,0.308114)
n=8 → 0.226797 → 0.977135 → (0.962279,0.169742)
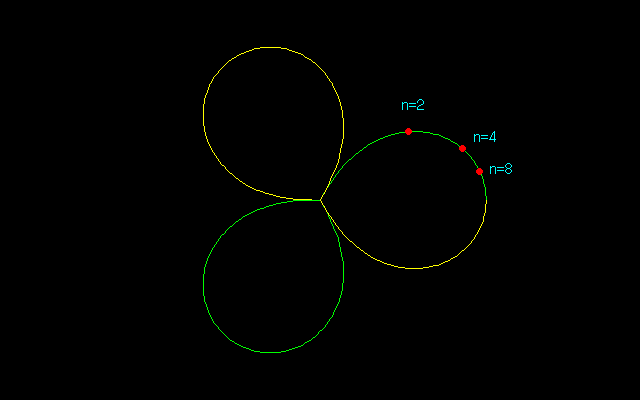
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
γ^2=1+mα^2+nα^4
として,減法公式を楕円曲線:y^2=1+mx^2+nx^4上の点(x,y),(α,γ)に適用すると,反転公式は
x’=(γx−α(1+mx^2+nx^4)^1/2)/(1−nα^2x^2)
で表される.
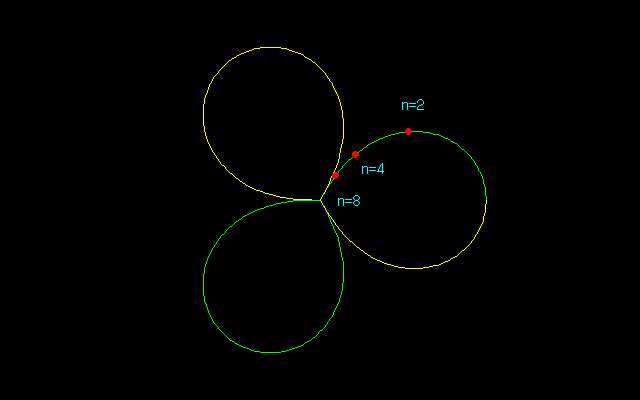
反転先はそれぞれ
x’ c (x,y)
n=2 → 0.732049 → 0.671621 → (0.53114,0.411053)
n=4 → 0.891288 → 0.348665 → (0.214279,0.275049)
n=8 → 0.934939 → 0.175156 → (0.09489,0.147226)
に移される.
===================================