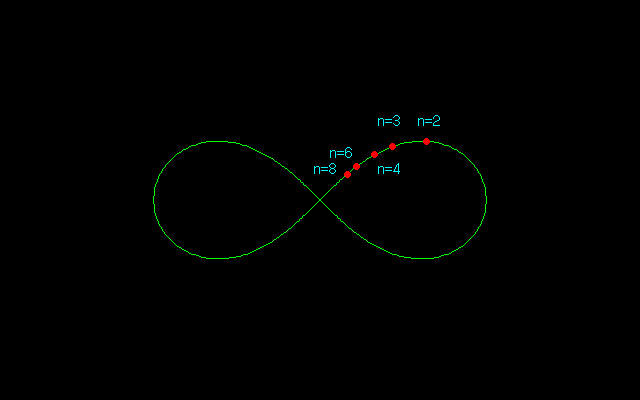
レムニスケート(連珠形)には円に共通する性質があり,定規とコンパスだけで奇数のn等分することができる必要十分条件はnがフェルマー素数(n=22^m+1の形の素数:3,5,17,257,65537)であることはよく知られている.ガウスはレムニスケートの等分問題から楕円関数を発見している.言い替えれば,方程式論には楕円関数論という背景があったのである.
しかし,この方程式を解くことは言うは易しいが,実行するにはかなり忍耐がいる.私も1回だけやってみたが結果はMathematicaなしには(私には)到達できなかったのも事実である.
今回のコラムでは,ベルヌーイのレムニスケートのn等分点を描いたので,それを掲載する.
[注]この図には誤りがあります.(その9)で訂正しています.

===================================
【1】作図とは,加減乗除と平方根である.
正多角形の作図は円周等分問題という幾何学問題ですが,x^n−1=0という代数方程式の解と密接な関係にあります.正5角形の作図は黄金比と関連していて,2次方程式:x^2−x−1=0を解く,すなわち(√5+1)/2を求めることによって可能となりました.ギリシャ人は黄金分割を用いた見事な方法で正五角形の作図に成功したのですが,この方法は二次方程式の幾何学的解法を利用した賢明な方法といえます.
一方,正7角形,正9角形はそれぞれ3次方程式:x^3+x^2−2x−1=0,x^3−3x+1=0に帰着します.また,立方体倍積問題,角の3等分問題,円の正方形化問題(円積問題)のいずれの幾何学的問題も代数方程式に対応していて,たとえば,倍積問題はx^3−2=0,角の3等分問題はx^3−3x−a=0,円積問題はx^2−π=0に帰着します.
定規とコンパスで描ける図形は直線と円ですから,その作図は線分の長さの加減乗除と平方根をとる操作に相当します.すなわち,定規(直線)とコンパス(円)による作図は,たとえそれらを繰り返し用いたとしても,+,−,×,÷,√なる5つの演算によって得られるものに限られています.
したがって,正7角形,正9角形の作図や倍積問題のように3次方程式に帰着する作図問題は+−×÷√の演算を組み合わせても解けません.角の3等分問題は,aの値によっては定規とコンパスのみで3等分できる角が無数にあると同時に,3等分できない角もまた無数にあることを示しています.モーリーの定理「任意の三角形において,各内角の3等分線の隣同士の交点を結んで得られる三角形は正三角形である.」この驚くべき定理が20世紀にいたるまで発見されなかった理由も,角の3等分問題は解けないことが判明していたところにあるのでしょう.
また,円積問題は2次方程式に帰着しますが,√πがコンパスと定規で作図できたとすると,その平方であるπも同様に作図可能ということになります.しかし,πは超越数ですから√πも超越数なのです.したがって,√πは代数方程式の解とはなりえず,円積問題も作図不能となるのです.
===================================
【2】正多角形の作図問題
定規とコンパスだけで正3角形,正4角形,正6角形,正8角形が作図できることは簡単にわかりますが,辺の数5,7,9の場合はどうでしょうか.正5角形は古代ギリシャにおいて作図可能であることが発見されました.となれば,次に正7角形・正9角形の作図は?と考えるのは自然な成り行きでしょう.
ところが,かのアルキメデスでさえも正7角形・正9角形の作図に成功しなかったといわれています.また,内接正多角形の作図は画家であり建築家であるレオナルド・ダ・ヴィンチの関心を惹きました.しかし,彼でさえ近似的な内接正七角形の作図を正確なものと思っていたようです.
辺数3,4,5,6,8,10,12,15,16の正多角形は作図できますが,辺数7,9,11,13,14の正多角形は作図できないことから,正17角形もそうであろうと推察されます.ところが,1796年,ガウスは19才のときに正17角形の作図を思いつき,のみならず,nが素数の正n角形について,n=22^m+1が素数の場合に限り,定規とコンパスだけで作図可能であることを発見しています.
正7角形も正9角形も作図できないのに,まさか正17角形が作図できるとはと思うのが普通なのでしょうが,このことを用いると,m=0のとき正3角形,m=1のとき正5角形,m=2のとき正17角形となり,作図可能であることがわかります.当然,ずっと面倒になるでしょうが,正257角形(m=3),正65537角形(m=4)も作図可能です.
アルキメデスは円柱とそれに内接する球の体積比が3:2であることを発見した記念に,自分の墓の上に円柱の形をした記念碑をおくように遺言したといわれています.アルキメデスと同じように,ガウスは正17角形を墓石に彫るよう遺言しています.このことはガウス自身がその発見をいかに重視したかを物語っています.数々の大発見をしたガウスですが,19才の青年がアルキメデスをもってしてもできなかった古代ギリシア以来2000年の謎を解いたのですから,まさに驚きとしかいいようがありません.この正17角形の作図は彼を本格的に数学の道に入らせるきっかけとなったといわれています.
なお,22^m+1の形の素数をフェルマー素数といいます.フェルマー素数はガウスによって1世紀にわたる眠りから覚まされ,数論と幾何学に新たな美しさを吹き込んだことになります.フェルマーはこの型の数がすべて素数だと勘違いしていて必ず素数を与える式として考え出されたのですが,m=5のときは素数ではなく,現在,m=0,1,2,3,4の5個以外にフェルマー素数はみつかっていません.6番目のフェルマー素数の探索がコンピュータを使ってなされていますが,はたして本当に存在するのでしょうか.
===================================
【3】代数的可解性の判定
5次以上の一般代数方程式は代数的に解けないことがアーベルによって証明されたわけですが,根の公式がないからといって数値解法以外に手段がないわけではありません.
たとえば,x^5−1=0は,
(x−1)(x^4+x^3+x^2+x+1)=0
と因数分解されますから代数的に解けます.一般に,n次の円分方程式:
x^n−1=0
は何次でも代数的に解けることがガウスによって証明されたのですが,ガウスは,この考察から正17角形の作図可能性をも発見しました.2次方程式の解ならコンパスと定規で作図可能なのですが,16次方程式:
x^16+x^15+・・・+x+1=0
x^8+x^7+・・・+x+1+1/x+・・・1/x^7+1/x^8=0
奇数n=2m+1に対して,n次方程式x^n−1=0は新しい変数としてy=x+1/xをとることによって方程式の次数をm=(n−1)/2次に減らせた方程式に帰着されますが,最終的には2次方程式に分かれてしまうので,正17角形は作図可能なのです.
それに対して,
x^5−80x−5=0
は代数的には解けない方程式です.いかなる条件の下で方程式は解きうるか?...このように,具体的に係数が与えられた方程式の代数的可解性を判定する問題が残っていたのです.
===================================
【4】おまけ(Gegoroのレムニスケート)
ベルヌーイのレムニスケートは三角関数を用いて
x=cosθ/(1+sin^2θ)
y=sinθcosθ/(1+sin^2θ)
とパラメトライズされるが,阪本氏によるとGegoroのレムニスケート
x=sinθ
y=sinθcosθ
というのもあるそうだ.以下にGegoroの連珠形を掲げる.
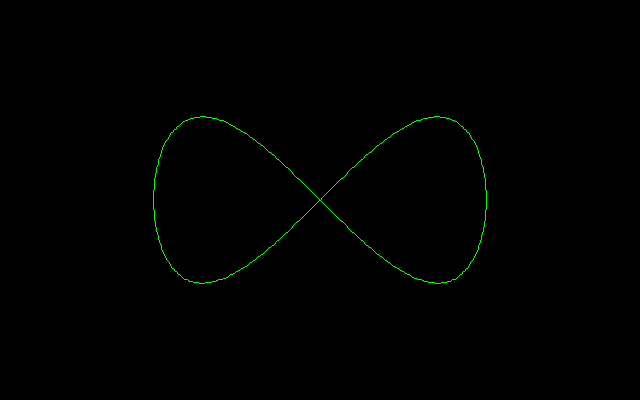
===================================