1週間ほど中国に滞在した後パソコンが壊れたため,しばらく掲載をお休みしていのだが,薄れかけた記憶をたどりながら再開することにしたい.
ルーローの四角形は擬内転形であるが,頂点の位置が1%ずれただけでも内転形でないことが一目瞭然となる.このことから内転形からのズレはごくわずかであることがわかる.今回のコラムでは(その42)で場合分けが煩雑となり中断した五角の穴をあけるドリルの内転形からの誤差を計算してみることにした.
===================================
【1】パラメータの説明
ルーローのn−1角形(nは奇数)の円弧の中心角を2α,頂角をβとする.
α=arctan(1/2・tanπ/(n−1))
β=2arctan(1/2・tanπ/(n−1))+π(n−3)/(n−1)
ω=2π/n
n=5 → α=26.565°,β=143.13°,ω=72°
また,正n角形の高さをH,正n角形の内接円の半径をr1,ルーローのn−1角形の弧の曲率半径r0,中心角を2α,正n−1角形の内接円の半径をr2とおくと,
r0cosα=2r2
r0(1+sinαtanπ/n)=r1(1+secπ/n)=H
n=5 → r0=H/(1+sinαtanπ/5)
r1=H/(1+secπ/5)
r2=Hcosα/2(1+sinαtanπ/5)
ルーローの四角形は区分毎に円弧を接続した曲線であるが,接線極座標を用いると各部分の継ぎ目でθをジャンプさせずに接続させることができる.区間毎の接線極座標表示を
p1(θ)=r0−r0cosθ
p2(θ)=−(r0−2r2)cosθ+r2sinθ
p3(θ)=r0−(r0−r2)cosθ−r2sinθ
p4(θ)=−r0cosθ+r2sinθ
p5(θ)=r0−(r0−2r2)cosθ
p6(θ)=−r0cosθ−r2sinθ
p7(θ)=r0−(r0−r2)cosθ+r2sinθ
p8(θ)=−(r0−2r2)cosθ−r2sinθ
p9(θ)=r0−r0cosθ=p1(θ)
とおいて,絶対誤差
f(θ)=Σ(k=0~n-1)p(θ+kω)−nr1
と相対誤差
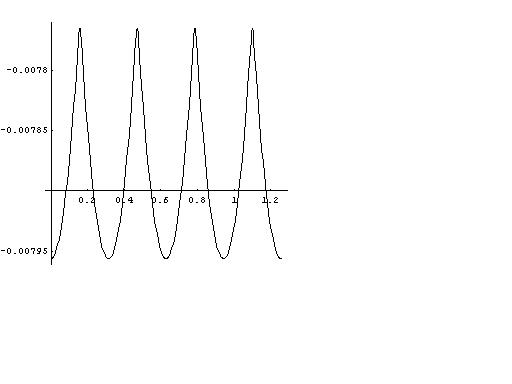
g(θ)=f(θ)/nr1
を計算してみる.ここでは,H=10とおいて誤差を求めることにした.
===================================
【2】区間毎計算
(1)0≦θ≦7α+3(π−β)−4ω(8.565)のとき
f(θ)=p1(θ)+p3(θ+ω)+p4(θ+2ω)+p6(θ+3ω)+p7(θ+4ω)−5r1
(2)7α+3(π−β)−4ω≦θ≦3α+2(π−β)−2ω(9.435)のとき
f(θ)=p1(θ)+p3(θ+ω)+p4(θ+2ω)+p6(θ+3ω)+p8(θ+4ω)−5r1
(3)3α+2(π−β)−2ω≦θ≦α(26.565)のとき
f(θ)=p1(θ)+p3(θ+ω)+p5(θ+2ω)+p6(θ+3ω)+p8(θ+4ω)−5r1
(4)α≦θ≦5α+3(π−β)−3ω(27.435)のとき
f(θ)=p2(θ)+p3(θ+ω)+p5(θ+2ω)+p6(θ+3ω)+p8(θ+4ω)−5r1
(5)5α+3(π−β)−3ω≦θ≦3α+(π−β)−ω(44.565)のとき
f(θ)=p2(θ)+p3(θ+ω)+p5(θ+2ω)+p7(θ+3ω)+p8(θ+4ω)−5r1
(6)3α+(π−β)−ω≦θ≦7α+4(π−β)−4ω(45.535)のとき
f(θ)=p2(θ)+p3(θ+ω)+p5(θ+2ω)+p7(θ+3ω)+p8(θ+4ω)−5r1
(7)7α+4(π−β)−4ω≦θ≦5α+2(π−β)−2ω(62.565)のとき
f(θ)=p2(θ)+p4(θ+ω)+p5(θ+2ω)+p7(θ+3ω)+p9(θ+4ω)−5r1
(8)5α+2(π−β)−2ω≦θ≦α+(π−β)(63.435)のとき
f(θ)=p2(θ)+p4(θ+ω)+p6(θ+2ω)+p7(θ+3ω)+p9(θ+4ω)−5r1
(9)α+(π−β)≦θ≦ω(72)のとき
f(θ)=p3(θ)+p4(θ+ω)+p6(θ+2ω)+p7(θ+3ω)+p9(θ+4ω)−5r1
===================================
【3】計算結果のまとめ
パソコンが壊れたこともあって,実際の数値計算は阪本ひろむ氏に担当してもらった.予想通り,「ルーローの四角形」の内転形からの相対誤差は1%未満であり,その変動幅はさらに小さかった.

この結果から,おそらくどのような円弧四角形も内転形にはならないものと思われる.しかしながら「ルーローの四角形」の内転形からの誤差はすこぶる小さいことがわかっただけでもその価値は大きいはずである.
なお,円弧から構成されている内転形(ルーロー曲線)を調べてきたが,どんな内転形も円弧から構成されていると誤解してはならない.フルヴィッツ・藤原曲線のように円弧でない内転形も存在するのである.
===================================