■ルーレット曲線の問題(その4)
【1】サイクロイド弧長のn等分
2r(−2cos(t/2)+2)=8r/n
−2cos(t/2)+2=4/n
cos(t/2)=1−2/n
y=r(1−cost)=r(2−2cos^2(t/2))=2r(1−(1−2/n)^2)
[1]3等分する場合,
y=2r・8/9,t=2arccos1/3
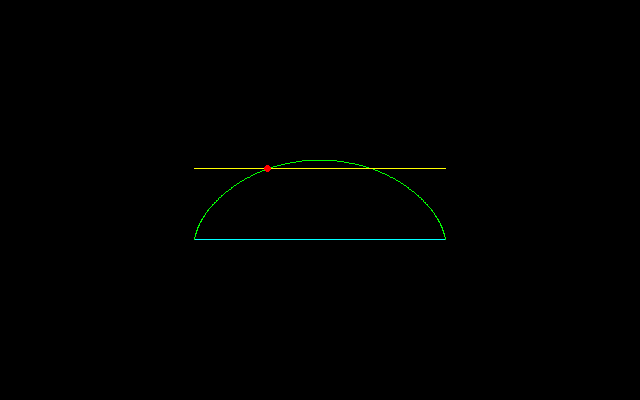
[2]4等分する場合,
y=2r・3/4,t=2arccos1/2=2π/3
===================================
【2】内サイクロイド弧長のm等分
4(n−1)/n(−cos(nt/2)+1)=8(n−1)/mn
−cos(nt/2)+1=2/m
cos(nt/2)=1−2/m
r^2=x^2+y^2=(n−1)^2+1+2(n−1)cosnt=(n−1)^2+1+2(n−1){2cos^2(nt/2)−1}=(n−1)^2+1+2(n−1)(1−8/m−8/m^2)
[1]3等分する場合,
r^2=(n−1)^2+1−14(n−1)/9
t=2/n・arccos1/3
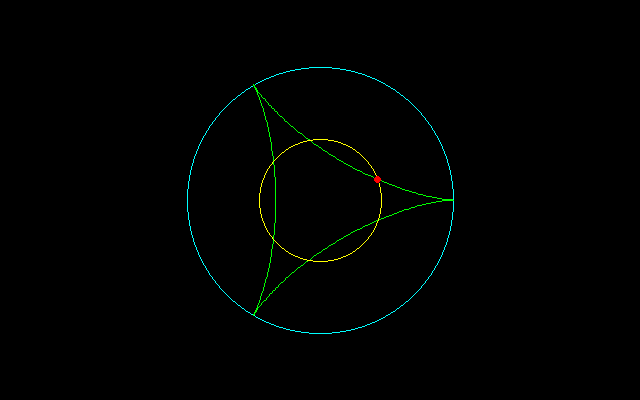
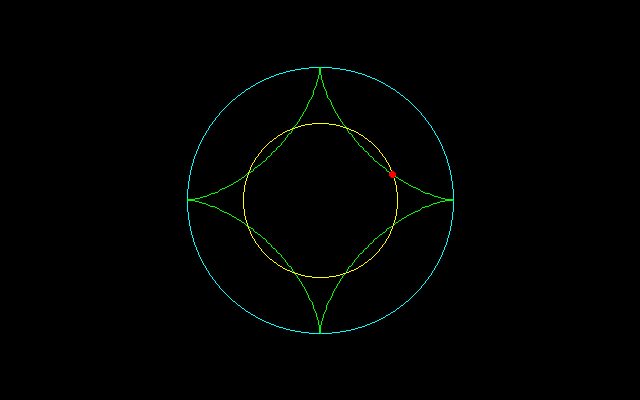
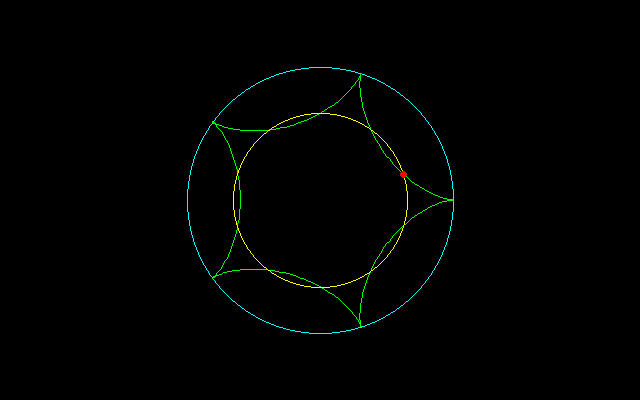

[2]4等分する場合,
r^2=(n−1)^2+1−(n−1)
t=2/n・arccos1/2=2π/3n
===================================
【3】外サイクロイド弧長のm等分
4(n+1)/n(−cos(nt/2)+1)=8(n+1)/mn
−cos(nt/2)+1=2/m
cos(nt/2)=1−2/m
r^2=x^2+y^2=(n+1)^2+1−2(n+1)cosnt=(n+1)^2+1−2(n+1){2cos^2(nt/2)−1}=(n+1)^2+1−2(n+1)(1−8/m−8/m^2)
[1]3等分する場合,
r^2=(n+1)^2+1+14(n+1)/9
t=2/n・arccos1/3
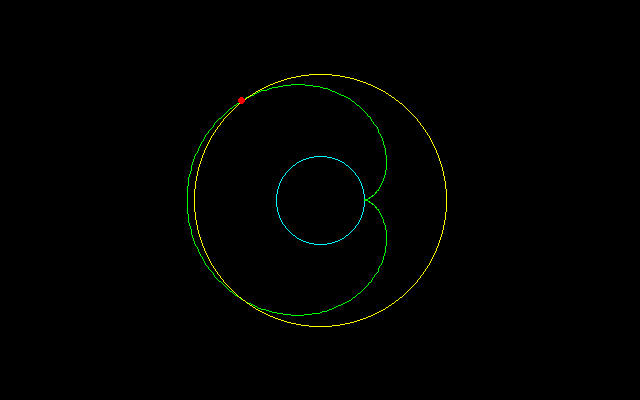
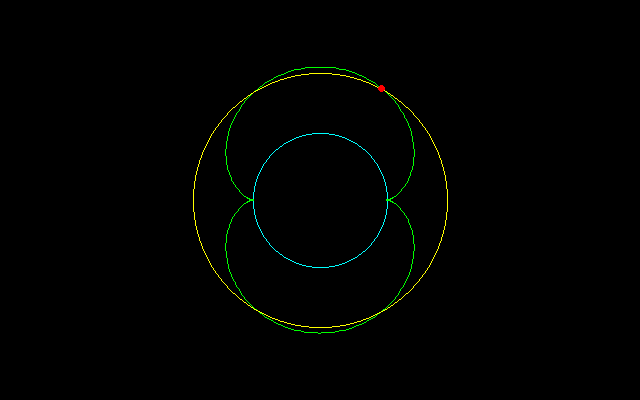
[2]4等分する場合,
r^2=(n+1)^2+1+(n+1)
t=2/n・arccos1/2=2π/3n
===================================
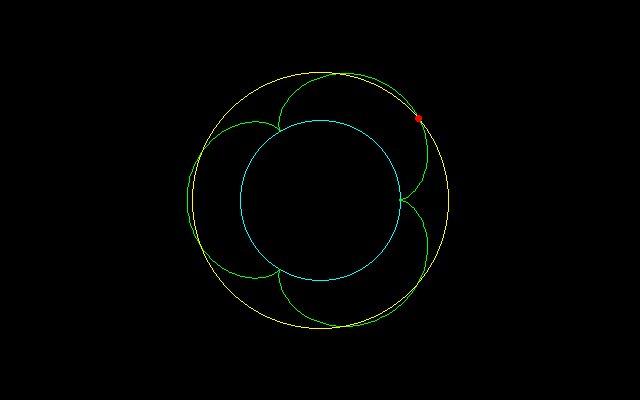
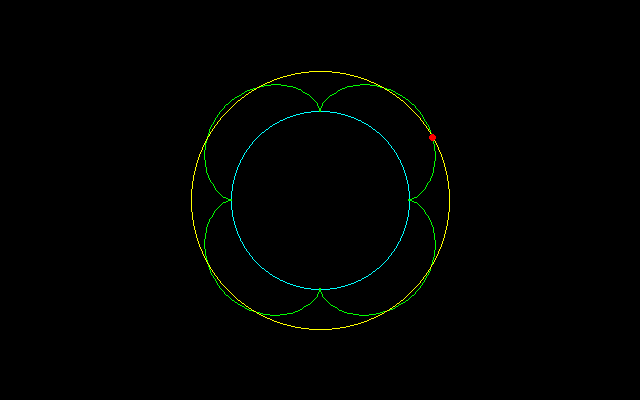
ルーレット曲線のうち,エピサイクロイド
x=acosθ−cos(a+1)θ
y=asinθ−sin(a+1)θ
aは固定円の半径,回転円の半径1
において,aが正の整数ならばa個の弧からなる閉曲線になります(a=1がカージオイド,a=2がネフロイド).この曲線のθ=0からθ=αの弧長は 4(a+1)/a・(1−cos(aα/2))
と表され,全長は8(a+1)です.
a=2^kのときには,cos(2^kα)が決まれば,cosα,sinα(したがってcos(a+1)α,sin(a+1)も)がそれから定規とコンパスで作図できるので,任意等分点が作図可能です.a=3だとcos(3α/2)からcosαを作図するには「角の三等分」が必要になり,定規とコンパスだけでは無理なようです.
ただ,カージオイド以外にもいろいろ任意等分が可能な曲線があるように存じます.
===================================











