レムニスケートには円に共通する性質があり，定規とコンパスだけで奇数のｎ等分することができる必要十分条件はｎがフェルマー素数（ｐ＝２^2^m＋１の形の素数：３，５，１７，２５７，６５５３７）であることである．

　これまで調べた曲線では

［１］任意等分可能・・・・・・カージオイド

［２］２^mΠｐi 等分可能・・・円，レムニスケート

［３］２^m等分可能・・・・・・ｒ^3/2＝ｃｏｓ（３θ／２），ｒ^3＝ｃｏｓ（３θ）

［４］２等分すら不可能・・・・ｒ^5/2＝ｃｏｓ（５θ／２）

となっていたが，これらはどのように特徴づけられるのであろうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】サイクロイド弧長のｎ等分

　　２ｒ（−２ｃｏｓ（ｔ／２）＋２）＝８ｒ／ｎ

　　−２ｃｏｓ（ｔ／２）＋２＝４／ｎ

　　ｃｏｓ（ｔ／２）＝１−２／ｎ

ｔが４直角の整数分の１になるのは，ｎ＝２とｎ＝４のときのみです．

［１］ｎ＝２のとき，ｔ／２＝π／２→ｔ＝π（ｙ＝２ｒ）

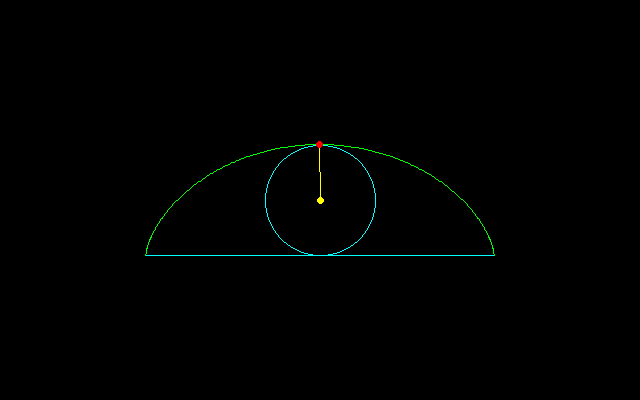
［２］ｎ＝４のとき，ｔ／２＝π／３→ｔ＝２π／３（ｙ＝３ｒ／２）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

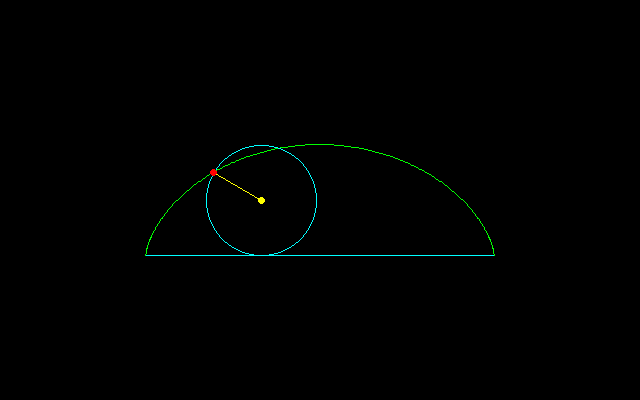
　サイクロイド弧長が２等分，４等分されることをみた．次に，

　　大円の半径：ｎ，小円の半径：１　　　（０＜ｔ＜２π／ｎ）

とする内サイクロイド

　　ｘ＝（ｎ−１）ｃｏｓｔ＋ｃｏｓ（ｎ−１）ｔ

　　ｙ＝（ｎ−１）ｓｉｎｔ−ｓｉｎ（ｎ−１）ｔ

と外サイクロイド

　　ｘ＝（ｎ＋１）ｃｏｓｔ−ｃｏｓ（ｎ＋１）ｔ

　　ｙ＝（ｎ＋１）ｓｉｎｔ−ｓｉｎ（ｎ＋１）ｔ

について調べてみたい．

【２】内サイクロイド弧長のｍ等分

　　∫(0,2π/n)（ｘ’^2＋ｙ’^2）^1/2ｄｔ

　＝√２（ｎ−１）∫(0,2π/n)（１−ｃｏｓｎｔ）^1/2ｄｔ

　＝２（ｎ−１）∫(0,2π/n)ｓｉｎ（ｎｔ／２）ｄｔ

　＝４（ｎ−１）／ｎ［−ｃｏｓ（ｎｔ／２）］＝８（ｎ−１）／ｎ

　　４（ｎ−１）／ｎ（−ｃｏｓ（ｎｔ／２）＋１）＝８（ｎ−１）／ｍｎ

　　−ｃｏｓ（ｎｔ／２）＋１＝２／ｍ

　　ｃｏｓ（ｎｔ／２）＝１−２／ｍ

　ｔが４直角の整数分の１になるのは，ｍ＝２とｍ＝４のときのみです．

　　ｃｏｓ（ｎｔ／２）＝１−２／ｍ

　　ｍ＝２のとき，ｎｔ／２＝π／２→ｔ＝π／ｎ

　　ｍ＝４のとき，ｎｔ／２＝π／３→ｔ＝２π／３ｎ

　　ｒ^2＝ｘ^2＋ｙ^2＝（ｎ−１）^2＋１＋２（ｎ−１）ｃｏｓｎｔ

＝（ｎ−１）^2＋１−２（ｎ−１）＝（ｎ−２）^2　　　ｔ＝π／ｎのとき

＝（ｎ−１）^2＋１−（ｎ−１）　　　　ｔ＝２π／３ｎのとき

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

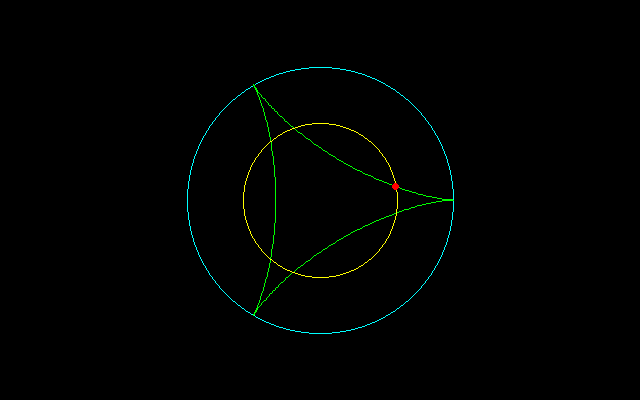
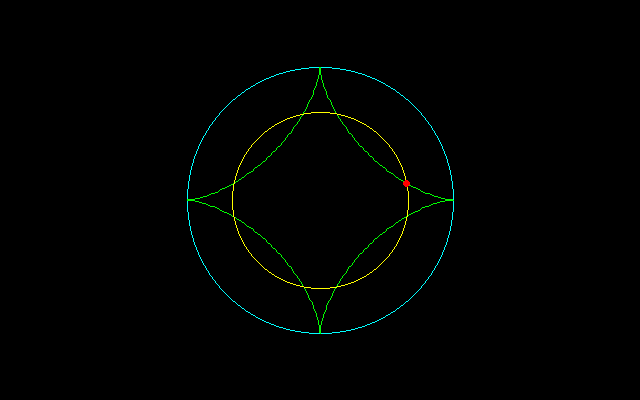
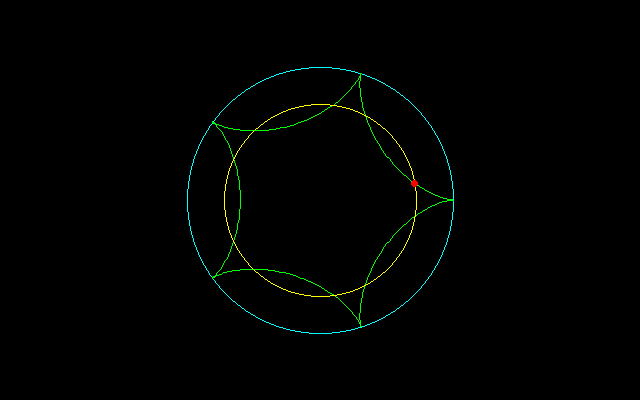
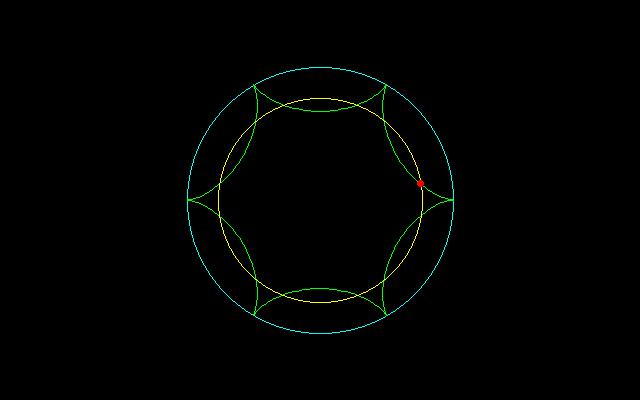
【３】外サイクロイド弧長のｍ等分

　　∫(0,2π/n)（ｘ’^2＋ｙ’^2）^1/2ｄｔ

　＝√２（ｎ＋１）∫(0,2π/n)（１−ｃｏｓｎｔ）^1/2ｄｔ

　＝２（ｎ＋１）∫(0,2π/n)ｓｉｎ（ｎｔ／２）ｄｔ

　＝４（ｎ＋１）／ｎ［−ｃｏｓ（ｎｔ／２）］＝８（ｎ＋１）／ｎ

　　４（ｎ＋１）／ｎ（−ｃｏｓ（ｎｔ／２）＋１）＝８（ｎ＋１）／ｍｎ

　　−ｃｏｓ（ｎｔ／２）＋１＝２／ｍ

　　ｃｏｓ（ｎｔ／２）＝１−２／ｍ

　ｔが４直角の整数分の１になるのは，ｍ＝２とｍ＝４のときのみです．

　　ｃｏｓ（ｎｔ／２）＝１−２／ｍ

　　ｍ＝２のとき，ｎｔ／２＝π／２→ｔ＝π／ｎ

　　ｍ＝４のとき，ｎｔ／２＝π／３→ｔ＝２π／３ｎ

　　ｒ^2＝ｘ^2＋ｙ^2＝（ｎ＋１）^2＋１−２（ｎ＋１）ｃｏｓｎｔ

＝（ｎ＋１）^2＋１＋２（ｎ＋１）＝（ｎ＋２）^2　　　ｔ＝π／ｎのとき

＝（ｎ＋１）^2＋１＋（ｎ＋１）　　　　ｔ＝２π／３ｎのとき

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
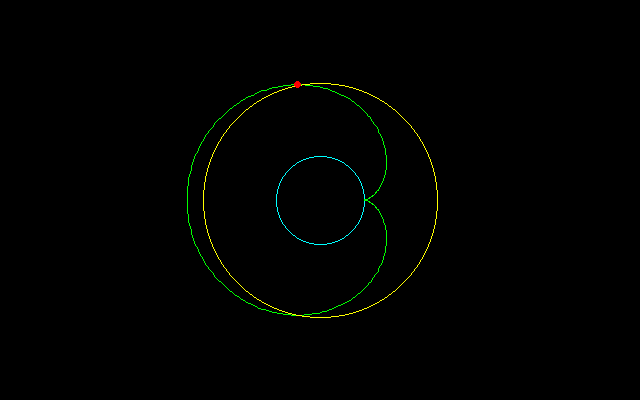
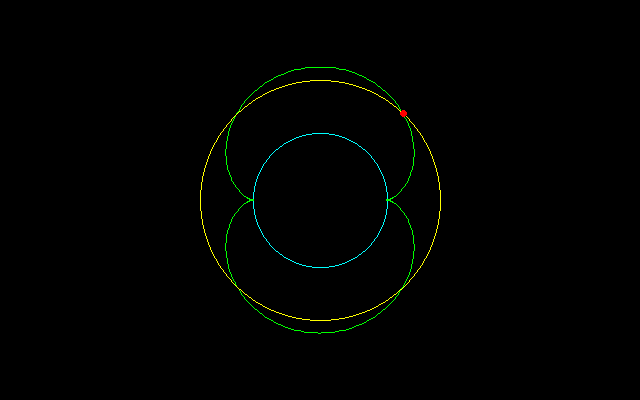