
アーベルとガロアは加減乗除とn乗根√,3√,4√,・・・を使って,5次方程式には根の公式がないことを証明したのですが,肺結核に侵され不幸にして夭折した天才アーベル,そして当時の数学界に受け入れられなかった悲劇の天才ガロアはわずか20才の1832年に決闘に倒れたことはあまりにも有名な悲話になっています.
アーベルとガロアが証明したことは一般的な5次方程式が係数の単純な演算を行う公式では解けないということであって,5次方程式が解けないという意味ではありません.1860年頃,ブリオスキ,エルミートらは超越関数である楕円モジュラー関数の5等分値を使って,初めて一般的な5次方程式を解くことに成功しました.
また,1870年代のクラインの研究は,正20面体を複素球面に内接させ,頂点,各面の中心,各辺の中点の座標の関係(正20面体方程式)を任意の5次方程式に還元させて,一般の5次方程式と特殊な6次方程式を解くのに成功しています.この5次方程式を多面体を使って調べるというアイディアは,
クライン「正20面体と5次方程式」シュプリンガー・フェアラーク東京
に紹介されています.
===================================
【1】正多面体の回転群
正多面体が5種類(正4面体,立方体,正8面体,正12面体,正12面体)しか存在しないことはギリシャ以来知られてきた.自然界の複雑さ・深遠さの一方で,古代の人々は5種類しか存在しない正多面体に神の摂理を見ていたのである.以下に,中川宏さん製作の木工正多面体模型を掲げる.

正多面体の回転を考えると,
(1)頂点と原点を通る軸を中心とした2πk/q回転 (k=1~q-1)
(2)辺の中心と原点を通る軸を中心としたπ回転
(3)面の重心と原点を通る軸を中心とした2πk/p回転 (k=1~p-1)
の3つが可能な回転軸である.
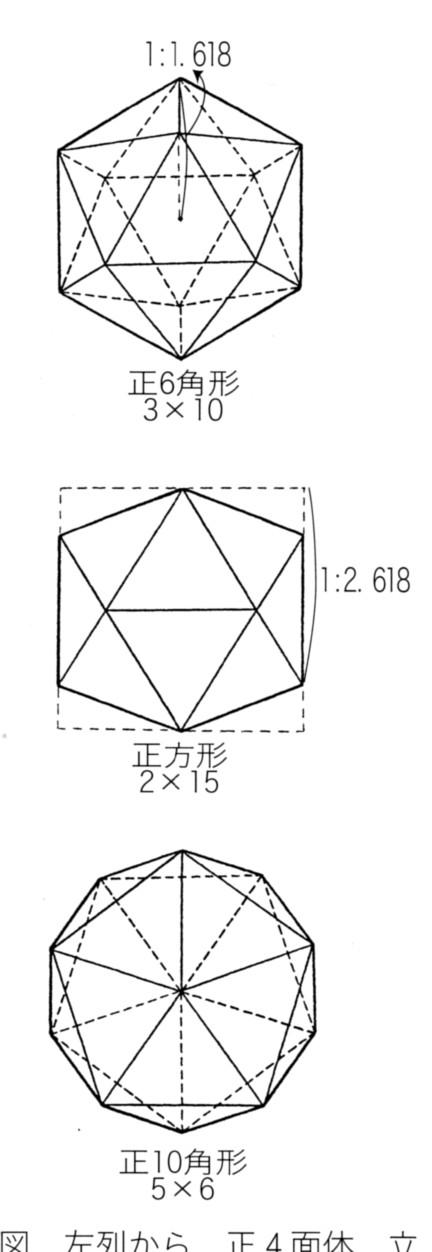
例として,正20面体の3心図を掲げる.上から順に面心図,辺心図,点心図であり,その投影図形はそれぞれ正6角形,歪6角形,正10角形になる.なお,正20面体の木工製作では辺心図が重要であり,面心図,点心図はあまり役に立たない.
[参]宮崎興二編著・石井源久・山口哲共著「高次元図形サイエンス」京都大学学術出版会
正20面体は20個の三角形面と12個の頂点,30個の辺をもつ.相対する面の中心同士を結ぶ直線を軸とする20種類の回転,相対する頂点同士を結ぶ直線を軸とする24種類の回転,相対する辺の中心同士を結ぶ直線を軸とする15種類の回転,それに恒等変換1種類,全部で
20+24+15+1=60
種類の回転がある.
これらの回転によって,正4面体(位数12)では4つの頂点の偶置換を引き起こすので4次交代群A4と同型,正8面体(位数24)では対面する面は4組あり,これらの組の置換を引き起こすので4次対称群S4と同型,正20面体(位数60)では30個の辺を5組に分ける偶置換として作用するので5次交代群A5と同型になることがわかる.
SO(3)の有限部分群A4,S4,A5はR^3の5種類の正多面体と密接な関係があり,S4は正6面体(正8面体:中心に関して点対称)を変えぬ運動の集合,A4は正4面体(点対称性はもたないが,面対称性をもっている)を変えぬ運動の集合,A5は正12面体(正20面体:中心に関して点対称)を変えぬ運動の集合であって,総称して「正多面体群」と呼ばれている.
正多面体の回転群は3次の特殊直交群SO(3)の有限部分群であるが,SO(3)にはこのほかに2種類の有限部分群がある.一つは巡回群,もうひとつは正2面体群であり,巡回群は正2面体群の部分群となっている.これらでSO(3)の有限部分群をつくすことが知られている.巡回群,正2面体群とA4,S4,A5とを併せて(広義の)正多面体群と呼ぶこともある.
以上より,SO(3)の有限合同変換群は,
(1)巡回群(Cn:位数n)
(2)正2面体群(D2n:位数2n)
(3)4次交代群(A4:位数12)←→正4面体群と同型
(4)4次対称群(S4:位数24)←→正6(8)面体群と同型
(5)5次交代群(A5:位数60)←→正12(20)面体群と同型
のいずれかである.
===================================
【2】クラインの見た正20面体(正20面体方程式)
幾何学に群を積極的に応用することを最初に主張したのが,クラインのエルランゲン・プログラム「幾何学とは変換群で不変な図形の性質を研究する分野」である.クラインは3次元空間内の回転対称図形は巡回群か,二面体群か,3種類の正多面体群(正四面体群,正八面体群,正二十面体群)のどれかに分類できることを証明した.
そして,方程式の根の置換群が正多面体群となるものを研究していたクラインは正20面体の回転群A5が5次方程式の根の置換群と同型であることを証明し,両者の意外な結びつきを「正20面体と5次方程式」の中で正多面体群と方程式論が交差する美しい小宇宙として論じている.
ところで,根号√,3√,4√,・・・という束縛を外すとどうなるのだろう.ベキ根によって解くとは方程式をz^n=aに帰着させるということであるが,たとえば,媒介変数tを導入してz=exp(t/n),a=exp(t)と書けば,指数関数と対数関数を用いて解を書き下すことができる.
そこで,5次方程式のよい媒介変数を見つけてその特殊関数によってその方程式を解くことが考えられる.5次方程式を正20面体方程式に帰着し,媒介変数を介して楕円モジュラー関数により解を求めるという方針に従って,楕円モジュラー関数
J(τ)=(1-240Σn^3q^n/(1-q^n)^3/12^3qΠ(1-q^n)^24,q=2πiτ
J5(τ)=q^(1/5)Σ(-1)^nq^(5n^2-3n)/2/Σ(-1)^nq^(5n^2-n)/2
を用いると,正二十面体方程式Φ(z)=aの解はJ(z)=a,z=J5(τ)と表される.
すなわち,5次方程式を正20面体方程式に帰着させれば,正20面体の対称性から保型関数を用いることができる.19世紀の後半,デデキントとクラインは独立に重さ0の保型関数
j(az+b/cz+d)=j(z)
ad−bc=1
を構成した.j(z)は最も簡単でよく知られているSL(2,Z)不変な保型関数で,q=exp(2πiz)とおくと,
j(z)=E4(z)^3/Δ(z)
=1/q+744+196884q+21493760q^2+864299970q^3+・・・
と展開される.J,J5は楕円モジュラー関数と呼ばれるものであり,
J(τ)=1/12^3(1/q+744+196884q+・・・)
J5はその5等分値である.
このようにして,クラインは5次方程式の回転群と楕円関数が絡み合った小宇宙で,5次方程式が特殊な楕円関数を用いて解ける理由を考察し,決定的な答えを導き出したのである.
[参]橋本義武「正20面体方程式」数学セミナー2007.1,日本評論社
===================================
【3】補遺
なお,現在では6次以上の高次元でも,モジュラー関数のような他の道具を使って解けることがわかっています.さらに,条件を厳しくした下で7次方程式を解くことはできるだろうかという問題も設定することができるのですが,それに対してはまだ解決の糸口すら見つかっていません.おぼろげながらも見えないので,現在,それを研究している数学者はほとんどいません.
===================================