ユークリッドは三角形の中心と呼べる点を４つ（内心，重心，外心，垂心）知っていたらしいのですが，これ以外にも中心はいろいろあります．

　微分積分の入門書に「平面上に３つの定点Ａ，Ｂ，Ｃがある．この平面上に点Ｐをとって，ＡＰ^2＋ＢＰ^2＋ＣＰ^2が最小になるようにせよ」という問題が偏導関数の応用例として載せられています．その点Ｐは重心です．３定点が４定点であっても，同じ議論になるのですが，距離の２乗の和に特に具体的な意味があるようには思えません．むしろ，２乗を取り去ったほうが問題としては自然です．

　そこで，「Ａ，Ｂ，Ｃ３軒の家に電線をひきたい．電線の長さを最小にするにはどこの柱を立てればよいか」ではＡＰ＋ＢＰ＋ＣＰを最小にする実用価値のある問題になります．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　１辺の長さが１の正三角形の頂点を考えてみる．正三角形の２辺に沿ってＡ→Ｂ→Ｃと電線をはわせると，電線の長さは２になる．しかし，正三角形の重心と３つの頂点のそれぞれとを結ぶことを考えると，電線の長さは√３で済む．

　一般の三角形についてのこの問題は１７世紀のフランスの数学者フェルマーがイタリアの物理学者トリチェリ，数学者カヴァリエリに出題したものとして有名な問題で，求める点Ｐをフェルマー点（またはトリチェリ点，シュタイナー点）といいます．点Ｐは三角形ＡＢＣの内部にありますが，∠Ａ，∠Ｂ，∠Ｃ＜１２０°のときには，３頂点に至る距離の和が最小となる点は３辺を等角１２０°に見込む点です．∠Ａ，∠Ｂ，∠Ｃのいずれかが≧１２０°のときには，それぞれ頂点Ａ，頂点Ｂ，頂点Ｃになります．

　このフェルマー点は頂点と外正三角形の頂点を結ぶ直線の共点として得られます．すなわち，フェルマー点を見つけるには与えられた三角形の各辺の上に正三角形を立てて各頂点と結ぶと，これら３本の線は１点Ｆで交わり∠ＡＦＢ＝∠ＢＦＣ＝∠ＣＦＡが成り立ちます．また，フェルマー点は３つの正三角形の外接円の交点でもあります．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　さらに一般の位置にある頂点の集合についてはどうだろうか？　１辺の長さが１の正方形の４つの頂点の場合でさえ，最短結線の仕方は自明ではない．正方形の３辺に沿ってＡ→Ｂ→Ｃ→Ｄと電線をはわせると，電線の長さは３になる．しかし，２点を加えると１＋√３が最短となることがわかっている．これ以上点を加えたとしても短くはならないのである．

　以下に，長さの総和を最短にする平面石鹸膜の３点，４点シュタイナー問題の解を示す．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

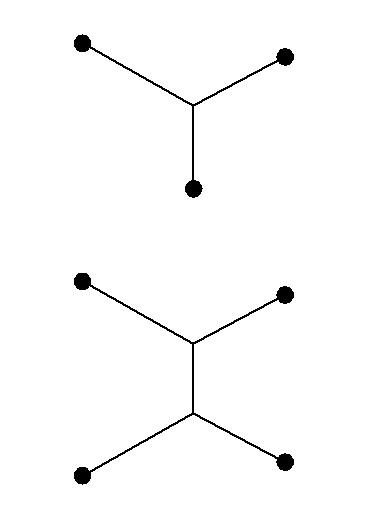
　それでは７×７格子，もっと一般にｎ×ｎ格子の場合はどうなるだろうか？　このような最短配線問題は最小木問題（問題の発案者シュタイナーに因んで最小シュタイナー木問題）と呼ばれていますが，ＶＬＳＩ回路を設計するときの最も基本的な技術となっています．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝