このコーナーでは中川宏さん製作の木工多面体をシリーズで取り上げてきましたが，つい最近，

　　中川宏「多面体木工」（非売品）

がＮＰＯ法人・科学協力学際センターから刊行されました．

　この書籍は一松信先生の傘寿のお祝いにするために，中川さんのオリジナリティーに富むお仕事を集大成したものです．中川さんの木工の原点にある２つの至宝とは「切稜立方体」と「正十二面体」のことですが，この本が３つ目の至宝ということになりました．

　中川宏さんのご厚意によりご希望の方にこの本を配布いたします．非売品ですので頒布価格は無料ですが，送料は負担していただきます．申し込み要綱は以下の通りです．

〇申込み先

　〒９８１−１２３９　宮城県名取市愛島塩手字野田山４７−１

　宮城県立がんセンター・研究所・病理　　佐藤郁郎

　　　　　ＴＥＬ 022(384)3151-333，ＦＡＸ　022-381-1138

　封書に送付先を記入，切手２９０円分を貼ってお送り下さい．

　数に限りがありますので，事前に下記までお問い合わせ願います．

〇問い合わせ先 佐藤（sato-ik510@pref.miyagi.jp）

　内容に関する質問は、ご質問内容を詳しくお書きのうえ書面かＦＡＸ，e-mailにてお願い致します。

〇関連画像取得先（長谷川浩さん製作）

(1)正１２面体の木工製作ＣＧ

http://geocities.jp/asobiwosentoya/pov/nakagawa/naka12c.html

(2)正１２面体の回転ＣＧ

http://geocities.jp/asobiwosentoya/pov/nakagawa/naka01a.mpg

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　この本は一松信先生の傘寿のお祝いに間に合わせるために，編集に関してはズブの素人の中川宏さんが急造されたものです（失礼！）．現在，中川宏さんはじっくり時間をかけて，ＮＰＯ法人・科学協力学際センター発行予定の仮題

　　「多面体木工」丸善

も鋭意準備中です．こちらは非売品ではありません．非売品の内容に，多くの分野の方々からの寄稿文を加えた科学読み物にする計画だそうです．

　たとえば，小生は商売柄「癌細胞はどのような形をしているのか？」という質問をよく受けるのですが，ザクロ，ハチの巣，石鹸の泡などのように，空間がある立体（多面体）によって分割される空間分割は，生物と無生物を問わず，自然界に広く見られる現象で，生物材料や石鹸の泡などでは１４面体の空間分割構造が実際に観察されます．

　１４面体が最も多いという実験的研究から，必然的に辺数５を中心とする分布をなすことが示唆されますが，このことは経験的に５角形の頻度が最も高いという観察結果に一致します．１４面体が得られる理由について考えてみると，実はこれも必然的に決定されることであって，２次元の格子の多くについてボロノイ細胞は六角形であり，３次元の格子の多くについてボロノイ細胞は１４面体であるのです．ついでにいうと，ボロノイ細胞の面の数ｆは原始的な格子に対するものが最大でｆ＝２（２^n−１）個ですから，４次元格子では３０，５次元格子では５２となります．

　　ｎ＝２　→　ｆ＝６

　　ｎ＝３　→　ｆ＝１４

　　ｎ＝４　→　ｆ＝３０

　　ｎ＝５　→　ｆ＝５２

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

　次に，安定な平面分割・空間分割という観点から考えてみることにしましょう．

　（問）正多角形は無限に多く存在しますが，それでは，互いに合同な正多角形を隙間も重なりもないように並べて平面を完全に埋める仕方が何通りあるでしょうか？

　（答）平面充填形は正三角形，正方形，正六角形の３種類に限ることは，昔からよく知られていますが，このうち正方形のは碁盤，正六角形のは蜂の巣などでおなじみでしょう．

　しかし，正三角形と正方形による平面分割は頂点だけで接している多角形があるので，ボロノイ分割に対して安定とはいえません．点のわずかな動きによって，ボロノイ分割が激変してしまうのです．したがって，ボロノイ分割の意味で安定なものは六角形による平面充填だけということになります．

　それでは，３次元ではどうでしょうか？　単独空間充填形となる多面体である立方体，菱形十二面体，切頂八面体のうち，１点に４個の多面体が会してボロノイ分割に対して安定なものは切頂八面体だけなのですが，立方体と菱形十二面体は，切頂八面体の辺を点に縮めることによって得られるというわけです．

　乱雑配置状態で等方的に圧縮すると，空間は多面体によって分割充填されることになります．この状態をrandom packingといいますが，大域的には乱雑配置状態であっても局所的には格子状配置を模するのであって，以上のことが１４面体が最も多いとする実験的研究から得られた値を裏付ける１つの根拠を与えてくれます．

　また，配置が完全に規則的である格子と完全にランダムな点の配置は対極的ではありますが，どちらも数学的な扱いが容易な構造であるということも理解されます．数学的にみると完全な「ランダムネス」は意外に扱いやすいのですが，このような内容を詳細に記述して寄稿しようと考えているところです．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［補］中川宏の２つの至宝

　「切稜立方体」は正多面体・準正多面体を製作するための足場となる重要な立体で，中川さんはこの立体のことをＥＣ細胞と呼んでおられます．ウマイ喩えです．

　「正１２面体」からは立方体に位相幾何学的変形を加えることによってあっというまに１２もの正五角形を作り出す木工マジックが体験できます．そのプロセスをタネアカシしますと，正１２面体の正投影図としては面心図，点心図，線心図の３種類がありますが，面心図は正１０角形，点心図は歪１２角形，線心図は歪６角形になります．

　このことから面心図が木工正１２面体の製作に役立ちそうにみえるのですが，実際に役立つのは線心図です．線心図に投影された線を延長すると正方形になるのですが，立方体の切稜角を３１．７１７５°に設定して削りとると正十二面体ができあがります．このことは正十二面体が立方体に内接し五角形の一辺を１とすると，外接立方体の一辺はφ^2であることから示されます．

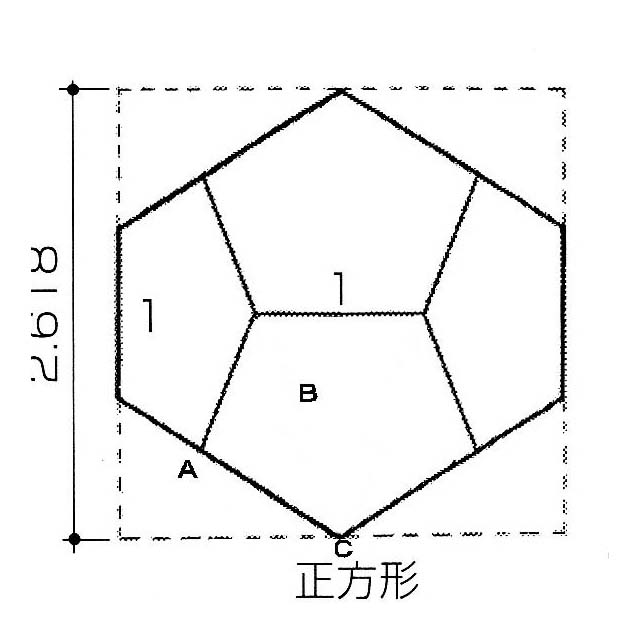
　その際，立方体の東西南北天地面のうち，天地面に対しては東西方向の辺だけ（南北方向の辺は削らない），東西面に対しては南北方向の辺だけ（天地方向の辺は削らない），南北面は天地方向の辺だけ（東西方向の辺は削らない）を３１．７１７５°で切稜して，もとの立方体表面の名残りとして１本の稜だけが残るようにします．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝