今回のコラムでは，ｎ角の穴をあけるドリルを具体的に実現させるために，ｎ＝４の場合の応用であるロータリーエンジンの機械運動学的解析から始めたい．ロータリーエンジンの工学機構は数学的に非常によく考えられていて感心させられる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】ロータリーエンジンの機械運動学的解析

　ルーローの三角形型のローターは芯のずれた軸（エキセントリックシャフト）に取り付けられ自由に回転するようになっている．また，ローターの回転を制御するため，軸のまわりで固定された回らない歯車（ステーター）のまわりをローターの内歯が噛み合うようになっている．

　ステーターはローターの中心の軌跡に一致するので，ローターの内径はステーターの外径の２倍である．また，ローターを１回公転する間に１／３回自転するという運動を実現させなければならない．

　そのためには，ローターの内歯数をｒ，ステーターの外歯数をｓとして

　　（ｒ−ｓ）／ｒ＝１／３　→　２ｒ＝３ｓ

であることが必要になる．たとえば，ｒ＝２４であればｓ＝１６ということになる．歯数の差によって，ローターの１回転（自転）で軸は３回転（公転）し，４サイクルエンジンの工程が進行するのである．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】ｎ角形の穴をあけるドリルの場合

　ｎ＞３ではローターの中心の軌跡は円もどきであるので，ローターの内径はステーターの外径の２倍であるという条件は変わらない．変わるのはローターを１回公転させる間に１／（ｎ−１）回自転させるというところである．

　したがって，

　　（ｒ−ｓ）／ｒ＝１／（ｎ−１）　→　（ｎ−２）ｒ＝（ｎ−１）ｓ

ｎが大きくなるにつれて，両者の歯数の差は小さくなることがわかる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【３】３角形の穴をあけるドリルの場合

　ｎ＝３ではローターの中心の軌跡は円からかけ離れてハイポトロコイドで近似される曲線になるのだが，ロータリーエンジンの機械運動学的解析から，ステーターは円でなくても，定幅図形であればよいことがわかる．

　定幅図形はいかなる方向に関しても等しい幅をもっているので，その幅の２倍の直径をもつ円の中心は，常に定幅図形の周上にあることになるからである．このことは定幅図形を水平線上で転がすと，回転の中心は直線との接点の鉛直線上にあることから理解される．

　「定幅図形」の例として

（例１）ルーローの三角形

　ルーローの三角形とは，一辺の長さａの正三角形（２次元単体）の各頂点を中心にして半径ａの円弧を描くと作られる，３つの円弧からなる等辺円弧三角形です．

（例２）ルーローの三角形の平行曲線

　また，各角内に半径ａ＋ｒ，各対角内に半径ｒの円を描いても定幅曲線が得られます．これはルーローの３角形上に中心をもつ定半径円群の包絡線であり，いわば，ルーローの三角形の「平行曲線」です．

（例３）ルーローの多角形およびその平行曲線

　正三角形の代わりに正（２ｑ＋１）角形についても同様です．

をあげておく．

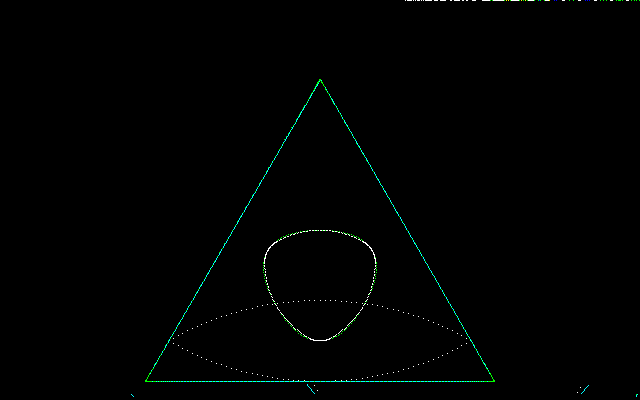
　ここで必要とされるものはハイポトロコイド近似ではなくて，定幅曲線近似である．以上のことから，藤原・掛谷の２角形の中心の軌跡（三角おむすび形の軌道）をルーローの三角形の平行曲線で近似することを考えてみる．藤原・掛谷の２角形の中心の真の軌道（緑）と近似軌道（白）をオーバーラップさせて示すが，両者はほぼ重なっていることがわかる．

　ロータリーエンジンの場合とは違って，藤原・掛谷の２角形のなかに定幅図形の幅の２倍の直径をもつ円をあけることはできないし，この円は三角形からさえもはみ出してしまうと思われるが，

　　（ｒ−ｓ）／ｒ＝１／２　→　ｒ＝２ｓ

の歯車機構をもたせることは可能だろう．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝