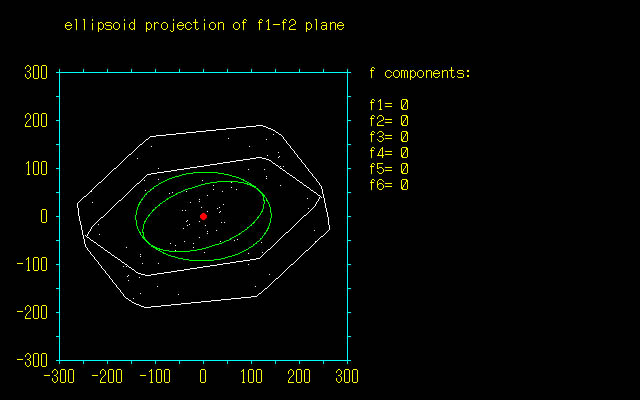
３次元空間の運動を表現する変数は６次元ベクトルになる．すなわち，ｘ軸方向・ｙ軸方向・ｚ軸方向の並進，ｘ軸まわり・ｙ軸まわり・ｚ軸まわりの回転である．したがって，関節自由度が６であれば冗長自由度はなくなり，ヤコビアンは正方行列になる．

　ところが，人間の上肢の関節自由度は７自由度あり，そのため手先の位置と方向を決めても自由に腕を動かすことができる．このとき実に様々な姿勢をとることができるが，冗長自由度のおかげで作業空間における手先運動の要求を満たしつつ，障害物回避や特異点回避などの姿勢をとることができるのである．

　冗長でなければ与えられた関節トルクτとつり合う手先力Ｆは常に存在するが，冗長な場合は関節トルク空間を覆うことができないので必ずしも存在するとは限らない．

　たとえば，τを７×１の関節トルクベクトル

　　τ＝（ｔ1,ｔ2,ｔ3,ｔ4,ｔ5,ｔ6,ｔ7）’

とすると，冗長でなければｔiは

　　ｔimin≦ｔi≦ｔimax

なる直方体領域をわたるが，冗長な場合は関節トルク空間に制限がかかるので，この直方体領域すべてをカバーすることはできず有界な多面体（polytope）となるのである．

　今回のコラムでは，冗長度を考慮に入れてこの多面体のすべての頂点を求めてみることにした．すなわち，以下に掲げる多面体の頂点検索方法は本シリーズの解決篇ということになる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】問題点の整理

　　τ＝Ｊ’Ｆ

という関係式を考えます．ここで，Ｆは６×１の手先力ベクトル

　　Ｆ＝（ｆ1,ｆ2,ｆ3,ｆ4,ｆ5,ｆ6）’＝（Ｆ1,Ｆ2）’

で，Ｆ1＝（ｆ1,ｆ2,ｆ3）’が手先力，Ｆ2＝（ｆ4,ｆ5,ｆ6）’がモーメント．また，τは７×１の関節トルクベクトル

　　τ＝（ｔ1,ｔ2,ｔ3,ｔ4,ｔ5,ｔ6,ｔ7）’

であって，ｔiは

　　ｔimin≦ｔi≦ｔimax

なる直方体領域をわたります．Ｊは６×７のヤコビ行列です．

　冗長でなければＪの逆行列が一意に定まるため，

　　τ＝Ｊ’Ｆ

　　Ｆ＝（Ｊ’）^(-1)τ

が成り立ちます．

　冗長な場合は，左からＪをかけると

　　Ｊτ＝ＪＪ’Ｆ

ＪＪ’は正方行列ですから，逆行列（ＪＪ’）^(-1)が定義できて

　　Ｆ＝（ＪＪ’）^(-1)Ｊτ

したがって，（ＪＪ’）^(-1)ＪがＪ’の逆行列の役割をすることがわかります．そこで，Ｊ’のムーア・ペンローズ行列（疑似逆行列）を（Ｊ’）~と書くことにすると

　　（Ｊ’）~＝（ＪＪ’）^(-1)Ｊ

すなわち

　　Ｆ＝（Ｊ’）~τ･･･････(2)

となります．Ｊは６×７のヤコビ行列であって，（Ｊ’）~はその転置行列のムーア・ペンローズ行列を表します．これより（Ｊ’）~も６×７行列となります．

　ところが，ムーア・ペンローズ行列には次のような欠点があります．Ｆ→τ→Ｆと写像する場合，

　　（ＪＪ’）^(-1)ＪＪ’＝（Ｊ’）~Ｊ’＝Ｉ（単位行列）

となって元のＦの値にに戻るのですが，τ→Ｆ→τと写像する場合には，

　　Ｊ’（ＪＪ’）^(-1)Ｊ＝Ｊ’（Ｊ’）~≠Ｉ（単位行列）

となって元に戻るとは限らないのです．元に戻らない場合があるので「疑似逆行列」と呼ばれているのですが，逆行列の標準的な定義は，行列が正方行列ではない場合あるいは特異行列の場合には成り立たないのです．

　（その３）までは疑似逆行列解

　　Ｆ＝（Ｊ’）~τ　　　（Ｊ’）~＝（ＪＪ’）^(-1)Ｊ

を求めてみたのですが，この解は目的関数の２乗和を最小にする解ではあっても，一意でなく任意性

　　Ｆ＝（Ｊ’）~τ＋（Ｉ−（Ｊ’）~Ｊ’）η

　　　　ηは任意の７次元ベクトル

があることが欠点です．このことは，左からＪ’をかけると

　　Ｊ’Ｆ＝Ｊ’（Ｊ’）~τ＋（Ｊ’−Ｊ’（Ｊ’）~Ｊ’）η＝τ

となり，

　　Ｆ＝（Ｊ’）~τ＋（Ｉ−（Ｊ’）~Ｊ’）η

が一般解となっていることが確かめられます．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

　冗長の場合でもＦからτは一意に定まりますが，Ｊの逆行列が一意に定まらないため，τからＦは一意に定まりません．しかし，冗長な場合でも１対１の対応であるため，元の値と何らかの関係（幾何学的な関係）はあるはずです．

　元には戻るためには

　　Ｊ’（ＪＪ’）^(-1)Ｊ＝Ｊ’（Ｊ’）~＝Ｉ

となることが必要ですが，そこでＪの階数（ランク）をｒとしてＪを特異値分解（ＳＶＤ）してみることにします．

　　Ｊ＝ＵΣＶ’

　　　Ｕ＝［Ｕ1，Ｕ2］＝［ｕ1，・・・，ｕr｜ｕr+1，・・・，ｕ6］，ｕiは６次元ベクトル

　　　Ｖ＝［Ｖ1，Ｖ2］＝［ｖ1，・・・，ｖr｜ｖr+1，・・・，ｖ7］，ｖiは７次元ベクトル

　　　Σ＝［Ｄ｜０］

　　　　　［−＋−］

　　　　　［０｜０］

　　　Ｄ＝ｄｉａｇ（σ1，・・・，σr），ｄｉａｇは対角行列の意

　Ｕ，Ｖは直交行列ですから

　　Ｊ’＝ＶΣ’Ｕ’，Ｕ’Ｕ＝ＵＵ’＝Ｉ，Ｖ’Ｖ＝ＶＶ’＝Ｉ

より

　　ＪＪ’＝Ｕｄｉａｇ（σ1^2，・・・，σr^2）Ｕ’

と固有値分解され，

　　（ＪＪ’）^(-1)＝Ｕ’ｄｉａｇ（１／σ1^2，・・・，１／σr^2）Ｕ

　　Ｊ’（ＪＪ’）^(-1)Ｊ＝ＶＶ’＝Ｉ

となり，特異値分解を用いると元に戻ることがわかります．

　また，この結果より，ヤコビアンが特異値分解

　　Ｊ＝ＵΣＶ’

されている場合は，疑似逆行列を

　　Ｊ~＝ＶΣ~Ｕ’

と定義されたものとして扱うことが可能であることが理解されます．

　　Ｊ~Ｊ＝ＶΣ~Ｕ’ＵΣＶ’＝ＶＶ’＝Ｉ

　以上のことより

　　ＶＶ’＝Ｉ

なるＶを定める問題に帰着されたというわけです．

［補］特異値分解を用いると元に戻るのは，非正方行列の取り扱いに馴れていない小生にとっては摩訶不思議なことであり，まるでトリックでも見せられている感じがします．量子物理学において特異点を打ち消し無限大になるのを抑えながら計算する非常に巧みな方法がありますが，それに類似していると感じられるのです．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

　そこで，特異値分解の求め方を示しますが，実質的にはＵ1，Ｖ1，Ｄだけが関与し

　　Ｊ＝Ｕ1ＤＶ1’，Ｕ1’Ｕ1＝Ｉ，Ｖ1’Ｖ1＝Ｉ

ですから

　　Ｊ’ＪＶ1＝Ｄ^2Ｖ1

が成立します．

　この形はＡ＝Ｊ’Ｊに対する固有値問題（Ａｘ＝λｘ）と等価であって，ヤコビアンの特異値分解により容易にｒ本の直交する７次元基底ベクトルを得ることができます．すなわち，冗長性を考慮すると７次元の関節トルク空間が本質にｒ本の直交する７次元基底ベクトルで張られる部分空間に退化することになります．そしてとりもなおさずこの部分空間がわれわれの求める有界な多面体（polytope）というわけです．

　また，これまでみてきたように，この多面体は

　　τ＝Ｊ’Ｆ･･･････(1)

　　Ｆ＝（Ｊ’）~τ･･･････(2)

(1),(2)式どちらをも満足しますから，(1),(2)式で解の一意性が成り立つような（τからＦが一意に定まる）関節トルク空間となっています．そこで(1),(2)どちらをも満足するτ空間の頂点をはじめに探索し，その結果を(2)に代入してＦ空間の頂点を求めて最終的に凸包することにします．

　階数は正射影の場合ｒ＝６ですが，Ｆ2＝（ｆ4,ｆ5,ｆ6）’＝０なる切り口を求める場合にはｒ＝３となるだけで，考え方自体は正射影の場合とまったく同じになります．

［補］老婆心ながら申し添えておきますが，コラム「ロボットアームと６次元楕円体」で紹介した楕円体の描写では，

　　‖τ‖≦１→τ’τ≦１（７次元楕円）→Ｆ’ＪＪ’Ｆ≦１（６次元楕円）

ＪＪ’は６×６行列ですから，

　　ＪＪ’＝Ｕｄｉａｇ（σ1^2，・・・，σr^2）Ｕ’

と固有値分解され，これにより６次元楕円Ｆ’ＪＪ’Ｆ≦１の楕円半径や配向が定まります．

　その際，６次元楕円の正射影を求める問題と切り口を求める問題では考え方が表裏の関係にあると感じられたかもしれません．しかし，６次元楕円の正射影を求める＝６次元楕円の６次元切り口を求めてから２次元平面へ正射影する，６次元楕円の切り口を求める＝６次元楕円の３次元切り口を求めてから２次元平面へ正射影する，・・・，階数ｒの場合は６次元楕円のｒ次元切り口を求めてから２次元平面へ正射影すると考えることができるのであって，正射影も切り口もまったく同じ図式，同じ論法になっていることが理解されます．

　また，冗長な場合の楕円体の場合には，Ｊ~Ｊ＝Ｉがついて

　　τ’Ｊ~Ｊτ≦１（７次元楕円）

と表されるのですが，これは

　　Ｆ’ＪＪ~ＪＪ’Ｆ≦１　→　Ｆ’ＪＪ’Ｆ≦１

となって冗長でない場合と一致します．直観的にいえば，６次元楕円Ｆ’ＪＪ’Ｆ≦１は関節トルク空間の７次元楕円τ’Ｊ~Ｊτ≦１の６次元切り口を手先力空間へ射影したものと考えられるというわけです．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】多面体のすべての頂点を求めること

　ここまで到達できれば，あとはプログラム作りだけの問題となります．この多面体の頂点の座標をすべて漏れなく求めることにしましょう．そのためには７本の基底ベクトルで張られる直方体領域とｒ本の基底ベクトルで張られる空間の交点を求めることになるのですが，多面体は連立１次不等式

　　Σａijｘj≦ｂi

を満たす点の集合ですから，シンプレックス法を用いて頂点を探索する必要があるのではないかと考えられました．

　そうなれば評価関数をどのように設定したら求めたい領域を得ることができるのか，そのための評価関数の設定が難しく，特に高次元の場合，領域を漏れなく探索するのはかなりの難問だと思われました．しかし，結論を先にいうと冗長な場合は（式の数）＞（変数の数）なのでシンプレックス法は不要となり，この領域を漏れなくかつ短時間で求めるプログラムを作成することができました．

　７次元の場合をイメージするのは難しいので，３次元の場合について説明することにしますが，

(1)ｒ＝２では，３次元の直方体領域と２本の基底ベクトルで張られる平面の交点を求めることになる．この２次元平面は３次元直方体の辺（１次元）と交わるが，辺は２つの面の共通集合であって，最大値・最小値をとるパラメータ数は２である．

(2)ｒ＝１では，３次元の直方体領域と１本の基底ベクトルで張られる直線の交点を求めることになる．この１次元直線は３次元直方体の面（２次元）と交わるが，面では最大値・最小値をとるパラメータ数は１である．

　このことから演繹すると，７次元の場合

(3)７次元の直方体領域とｒ本の基底ベクトルで張られる空間の交点を求めることになる．この空間は７次元直方体の（７−ｒ）次元面と交わるが，そこでは最大値・最小値をとるパラメータ数はｒである．

　Ｖ1（７×ｒ行列）で張られる関節トルク空間は

　　τ＝ａ1ｖ1＋ａ2ｖ2＋・・・＋ａrｖr

と書けますから，以上のことより

　　τ＝Ｖ1ａ

　　Ｖ1 ＝［Ｖ11］

　　　　　［−−］

　　　　　［Ｖ12］

　　Ｖ11（ｒ×ｒ行列），Ｖ12（（７−ｒ）×ｒ行列）

　　τ＝（τ1，・・・，τr｜τr+1，・・・，τ7）’＝（Ｔ1，Ｔ2）’

のうち，Ｔ1に最大値ｔimax・最小値ｔiminの組，たとえば，

　　Ｔr＝（ｔ1max，ｔ2min，・・・，ｔr-1max，ｔrmin）

を割り当て

　　Ｖ11ａ＝Ｔr

から交点ａを求め，他の交点

　　Ｖ12ａ

が７次元直方体の領域内で交わるかどうかを判定すればよいことになります．

　その際，７個の式からｒ個の式を選び出す組合せ数は7Ｃr通り，ｒ個の式への最大値・最小値の割り振りは２^r通り，これらをすべて組み合わせて交点かどうかを判定すれば多面体のすべての頂点が求まることになります．

　最終的には，こうして求められたτから

　　Ｆ＝（Ｊ’）~τ

によって手先力空間Ｆが得られることになります．前述したように，一度

　　τ＝Ｊ’Ｆ

用いてτを求めてしまえば，冗長であろうとなかろうと

　　Ｆ＝（Ｊ’）~τ

式の解は一意に定まるのです．

　以上のようにすると，冗長の場合でもτからＦが一意に定まる関節トルク空間のすべての頂点が探索されたことになります．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

［補］７次元直方体の（７−ｒ）次元面の数は

　　２^r7Ｃr

で与えられます．交点の数はつねにこれより少ないというわけです．この値は多面体の頂点の個数に対する評価としては大きすぎると感じられるかもしれません．しかし，実際には7Ｃrを選び出す計算は非常に短時間で済みますし，２^rを選び出す方法は２^(r-1)に改善することができます．

　一般に，ｆkをｎ次元多面体のｋ次元面の数とし，

　　（ｆ0，ｆ1，・・・，ｆn-2，ｆn-1）

を構成要素とするｎ次元正多胞体では，組み合わせ的方法によって，ｋ次元胞数ｆkが求められます．たとえば，正単体では

　　ｆk＝（ｎ＋１，ｋ＋１）

なのですが，ｋ＝ｎ−１のときｆk＝ｎ＋１であって，胞数はｎ＋１と計算されます．同様に，双対立方体では

　　ｆk＝２^k+1（ｎ，ｋ＋１），ｋ＝ｎ−１のとき，ｆk＝２^n

立方体では

　　ｆk＝２^n-k（ｎ，ｋ），ｋ＝ｎ−１のとき，ｆk＝２ｎ

となります．

　もちろん，

　　正単体：ｆk＝（ｎ＋１，ｋ＋１）

　　双対立方体：ｆk＝２^k+1（ｎ，ｋ＋１）

　　立方体：ｆk＝２^n-k（ｎ，ｋ）

はオイラー・ポアンカレの定理：

　　ｆ0−ｆ1＋ｆ2−・・・＋（−１）^(n-1)ｆn-1＝１−（−１）^n

すなわち，ｎが奇数なら２，偶数なら０を満たします．この定理は正多胞体に限らず，ｎ次元凸多胞体について常に成立します．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【３】実行例

　プログラムを実行すると，最初に正射影，次に切り口が描写されます．それぞれ多面体と楕円体が描かれますが，両者を比較しやすいよう配慮したものです．

　多面体は

　　τ＝Ｊ’Ｆ

の係数をfor〜nextループで小刻みに変えること（マッピング）によっても得られます．それにはもちろん莫大な計算時間がかかりますが，・・・．ここで描いた正射影も切り口もマッピング計算で得られる値と一致しました．また，この方法で求められる領域は(1),(2)式も同時に満たされるため，疑似逆行列解

　　Ｆ＝（Ｊ’）~τ

よりも小さな領域となっていることも確認されています．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【４】雑感

　シンプレックス法を用いると検索漏れを防ぐことが難しいのではと思われましたので，別の方法を考え出しました．私の考えた方法は至極簡単なもので，多面体の頂点だけマッピングするという単純な発想です．

　（ｎ，ｍ）＝（３，２）の場合を見ていてシンプレックス法が不要であることに気づき，前述の方法で解けるのではというアイディアが浮かびました．それを（３，１）にしたり，（７，６）にしたり・・・．多分，大丈夫だろうとは思っておりましたが，実際に解けるかどうかはやってみなければわからない．プログラムを作る際には疑心暗鬼になったりもしましたが，見事に計算できることがわかりました．

　いわれてみれば誰でもわかるコロンブスの卵のようなものですが，何でこんな簡単な方法が思いつかなかったのか，いま思うと不思議です．これでやっと擬似逆行列解でない解が得られたので私もほっとしています．

　今回作成したプログラムの新規なる点を挙げろといわれれば，まず，高速計算可能ということです．最近のマシンならば三面図であっても１分以内に描けるでしょうから，これでデータを取りながらほぼリアルタイムでの多面体解析が可能になるものと思われます．

　もう一点，新規性についてアピールしておくと，冗長な場合でも多面体の頂点探索と正射影・切断面の取り扱いが可能となったのですが，楕円体では冗長であってもなくても正射影と切り口は変わりませんから，これで冗長な場合の

　　（多面体，楕円体）×（正射影，切り口）

のすべての組み合わせの描写法が揃ったことになります．比較しやすいようにとの配慮から，前掲の実行例ではこれらすべてを描いています．

　最後に，楕円体と多面体の性能比較をしておくと

　　　　　　　　　　楕円体　　　　　多面体

　　計算速度　　　　　高　　　　　　　低

　　計算精度　　　　　低　　　　　　　高

となります．すなわち，楕円体はあくまでも多面体の近似と考えられるわけですが，多面体よりも指向性を把握しやすいというメリットもあります．

　　　　　　　　　　楕円体　　　　　多面体

　　冗長性　　　　　無関係　　　　　関係

　　指向性　　　　　見やすい　　　　見にくい

　また，楕円体は生体向き，多面体はロボット向きともいえますが，先日，楕円体が手術用ロボットに応用されるようになったという話を聞き及び，このＨＰで紹介した楕円体や多面体の描写法が使われるようになるのはうれしいことと感じています．コラム

　　「ロボットアームと６次元楕円体」

　　「ロボットアームと６次元直方体」

　　「高次元の正多胞体」

も併せて読まれることをお勧めします．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝