平行四辺形の頂点と２等分点を使ったダイヤグラムでは，平行四辺形の重なりにおいて，４：５：３の比があらわれた．では，３等分点を使ったダイヤグラムではどうだろうか？

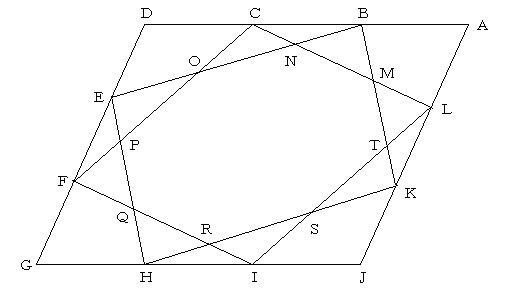
［１］求めるのは，ＥＯ：ＯＮ：ＮＢである．４：５：３になっていることは間違いなさそうであるが，証明してみよう．　　　（中川宏）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［証］

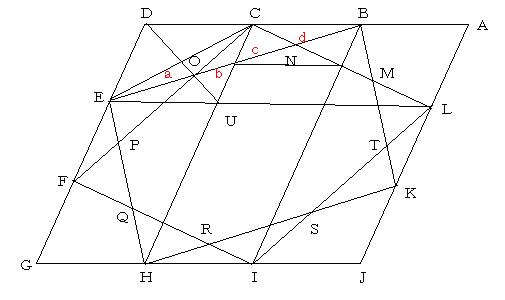
　三角形ＣＥＵにおいてＯは重心であるから，a:b=2:1

また，対角線ＢＥはＣＵによって２等分されているので，a+b=c+d

平行四辺形の対角線は相互に２等分するので，c=d

　そこでa+b+6とおくと，a=4,b=2,c=3,d=3

よって，ＥＯ：ＯＮ：ＮＢ＝４：５：３である．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［２］平行四辺形の対角線は，ほかの２頂点から対辺の３等分点にひいた４本の線分によって５：３：４：３：５に分けられる．

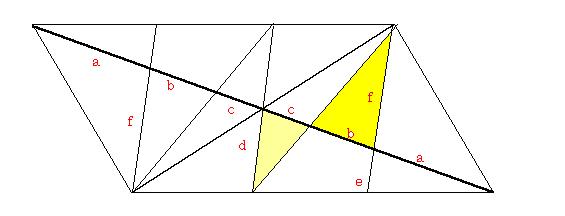
［証］上の図において，ｅ：ｄ：ｆ＝１：２：３

着色部分は相似図形なので，ｂ：ｃ＝ｆ：ｄ＝３：２

また，ａ＝ｂ＋ｃなので，ａ：ｂ：ｃ＝５：３：２

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

［３］三角形の中線は，他の頂点と対辺の３等分点とを結ぶ線分によって５：３：２に分割される．

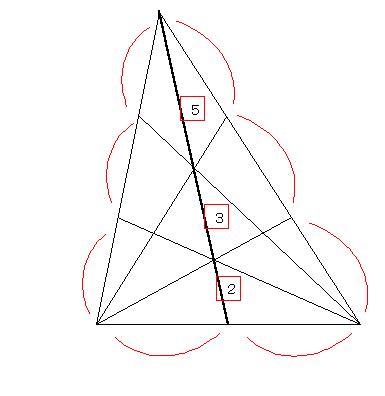
［証］２と同じことを三角形でいいかえればよい．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝