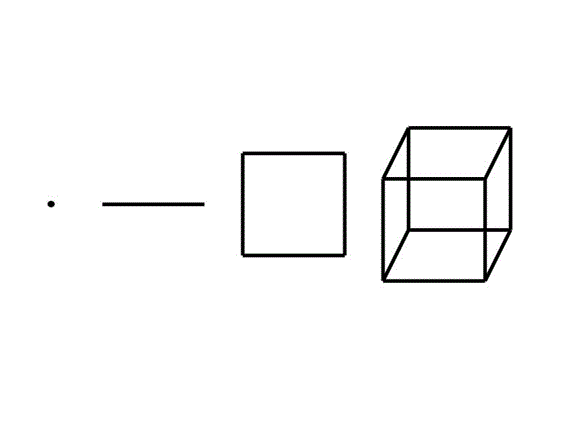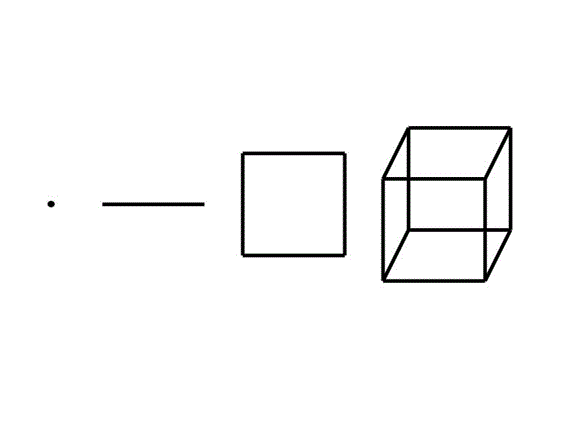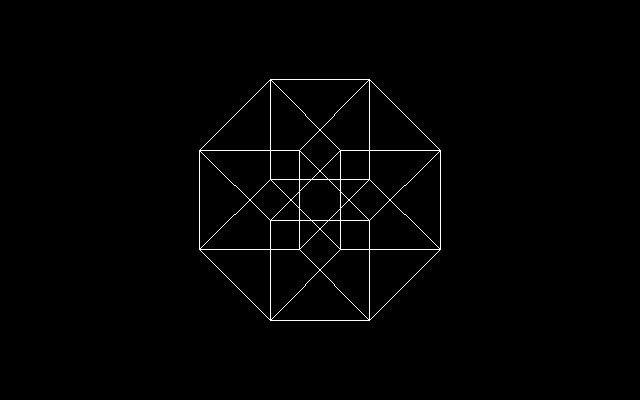■数学者に忘れられた問題(その2)
0次元の点がまっすぐ動くと1次元の線分になる.1次元の線分が平面の上で自分と直角の方向に同じ長さだけ動くと,2次元の正方形になる.2次元の正方形が3次元空間の中で自分と直角方向に1辺の長さだけ動くと,3次元の立方体となる.この3次元立方体が4次元空間の中で自分と直角方向に1辺の長さだけ動くと,同じ大きさの8個の立方体からなる4次元の立方体(正8胞体)になる・・・.このように,3次元立方体の8つの頂点を第4の方向に1単位だけ平行移動することにより,4次元立方体の3次元投影図を描くことができる.
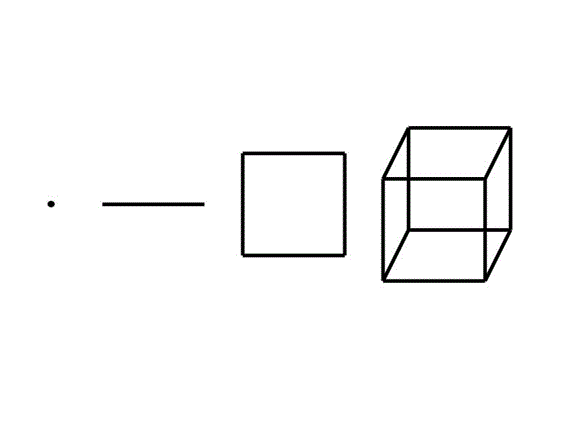
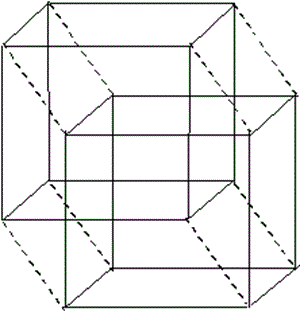
つまり,以下の図は4次元立方体の投影図というわけである.
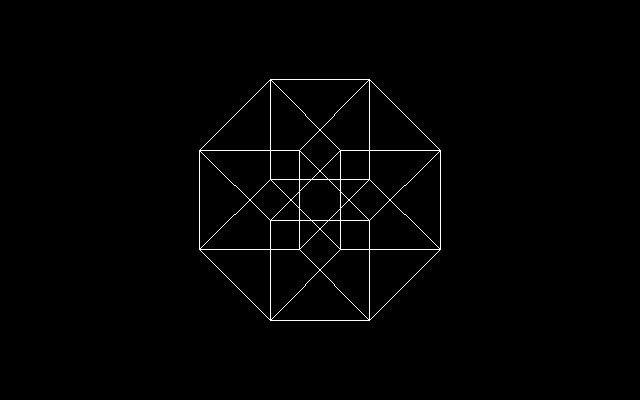
それを会社のロゴとしているところもある(イメージミッション社).

===================================
それでは次の図は何だろうか?

正五角形に対角線を描き入れると星形五角形(ソロモンの星)ができるが,正五角形と星形五角形の入れ子はペンタグラムと呼ばれる.
あるひとにとっては正五角形に適当に対角線を引いたように見えるかもしれない.黄金比は正五角形と密接な関係にある.正五角形に対角線を書き入れると星形五角形できるが,数学を知っている読者は,この手順を繰り返すと,正五角形と星形五角形が少しずつ縮小しながら無限に入れ子状になった図形を作ることができることを知っているだろう.また,グラフ理論を知っているひとならば,完全グラフK5と答えるかもしれない.しかし,それでもイメージは貧困である.
幾何学者にとっては,この図形は4次元正単体の投影図そのものなのである.もっといえば,n次元正単体は(n+1)個の点からなる完全グラフKn+1とみなすことができるのである.
もし,この図が5つの四面体の結合にみえたなら,あなたも立派な幾何学者である.
===================================
数学の世界には,ごく稀ですが,4次元や高次元の世界をイメージできる人がいます.たとえば,ペトリーは子供の頃から数学に対する異常な能力を示し,4次元図形を直観的に見ることができたといわれています.
しかしながら,3次元の世界を視覚化できるだけでも十分に希有な能力であって,数学者であっても2次元のイメージで何とかやっている人がほとんどです.実際,数学者であってもこの図形が4次元正単体の投影図であることを知っている人は(たとえいたとしても)少ないのです.
===================================