
これまで中川宏さんが木工製作した立体図形は,正多面体5種と準正多面体のうち「ねじれ立方体」「ねじれ12面体」を除く11種,その双対として菱形十二面体や菱形三十面体,4次元の正120胞体などです.
今回はまた中川さんにお願いして「ねじれ立方体」「ねじれ12面体」に挑戦してもらいました.ところが「ねじれ立方体」「ねじれ12面体」には平行な対面をもたない面があり,大変作りにくい立体であることがわかりました.
===================================
【1】ねじれ準正多面体の木工製作
ねじれ立方体(F=38,E=60,V=24)には中心に関して平行な対面をもたない24枚の正三角形面f3がある.正三角形面のうち8枚は4対の平行面となっているのであるが,それ以外の正三角形面は中心に対して平行な対面をもたないのである.
f3=24+8,f4=6
木工では平行な面あるいは直交する面があることが工作上の重要な点となっているのだが,プラトン立体とアルキメデス立体のなかでは正四面体,ねじれ立方体,ねじれ12面体を除いてすべて平行な対面をもっている.そのため,ねじれ立方体はすこぶる作りにくい立体となる.
この難点に対してはアイディアをもって克服するしかないのだが,ヒントは切稜切頂立方体にあった.切稜切頂立方体は切稜立方体の切頂あるいは切頂立方体の切稜によって作ることができるが,立方体を切稜してから切頂する場合,切頂の深さが切稜立方体の正方形面の頂点を越えると四角形面,六角形面,八角形面からなる26面体ができあがる.
コラム「朝鮮サイコロ・中国サイコロの数理」の(その8)で取り上げた大菱形立方八面体[4,6,8],(その9)で取り上げた内接球をもつ切稜切頂立方体(日本サイコロ)は切稜切頂立方体の例である.これらはもとの立方体の1辺の長さを2とし,切稜パラメータd1,切頂パラメータd2をそれぞれ
d1 d2
大菱形立方八面体 (6+2√2)/7 (12−3√2)/7
日本サイコロ 2(√2−1) 3−√3
と設定したものである.
また,原点から四角形面の中心までの距離は
H4=(d1/4+1/2)√2
原点から六角形面までの距離は
H6=√3(1−d2/3)
で与えられるから,それぞれの面までの距離は
四角形面 六角形面 八角形面
大菱形立方八面体 1.15301 1.09223 1
日本サイコロ 1 1 1
となる.
このようにd1,d2をうまく調節すると大菱形立方八面体では各面がすべて正多角形になるし,日本サイコロでは各面までの距離が等しくなるので内接球をもつことになる.
そこで立方体に対してうまく切稜,切頂を施すと四角形面,六角形面,八角形面に挟まれる頂点を取りまくそれぞれの対角線の長さを等しくすることができるはずである.すなわち変形[4,6,8]を中間産物として最終的にねじれ立方体[3,3,3,3,4]にたどりつくという着想である.

ねじれ12面体(F=92,E=150,V=60,f3=60+20,f5=12)に対してもこれと同様のアイディア,すなわち中間的に各面の対角線の長さの等しい変形[4,6,10]を作って,それを切って92面からなるねじれ12面体[3,3,3,3,5]を木工製作することにした.

なお,正四面体に切稜切頂操作を加えると切頂八面体[4,6,6]の変形立体ができるが,各面の対角線の長さを等しくした変形立体からは[3,3,3,3,3]すなわち正二十面体が得られる.ねじれ4面体を作ろうと思ってもよく知られた多面体となってしまい,この意味でのねじれ4面体は存在しないのである.
===================================
【2】ねじれ準正多面体の計量
当初はねじれ立方体に対して各頂点の座標を計算したのだが,ねじれ12面体についての座標計算は大変複雑になった.そこで座標を用いない方法を採ることにした.
ねじれ準正多面体のもとになる立体は(p,3)である.立方体のときp=4,正十二面体のときp=5となる.もとになる立体の1辺の長さをa,切稜パラメータをx,切頂パラメータをyとおくと,2p角形面と4角形面に挟まれる辺の長さは
b=a+2xcos(2π/p)−2x−2y
2p角形面と6角形面に挟まれる辺の長さは
c=2ycos(π/p)
4角形面と6角形面に挟まれる辺の長さは
d=2xcos(π/p)
で与えられる.
さらにこのことから,2p角形面の対角線の長さの2乗は
f(x,y)=b^2+c^2-2bccos(π(p-1)/p))・・・・・(1)
4角形面の対角線の長さの2乗は
g(x,y)=b^2+d^2・・・・・(2)
6角形面の対角線の長さの2乗は
h(x,y)=c^2+d^2+cd・・・・・(3)
で表される(余弦定理).
こうして(1)=(2)=(3)となるx,yを求める問題は4次方程式に帰着することが理解される.a=2とおいて実際に計算すると,
立方体 正十二面体
切稜パラメータx 0.456311 0.520868
切頂パラメータy 0.248091 0.268053
となった.
また,2p角形面間距離を1とおいた場合の各面間距離やもとの正多面体とねじれ準正多面体の1辺の長さの比は
四角形面間距離 1.09155 1.05863
六角形面間距離 1.06191 1.04855
2p角形面間距離 1 1
1辺の長さの比 0.437593 0.562122
と計算された.
(1)=(2),(2)=(3),(3)=(1)なる曲線を平面上に描くと円錐曲線(楕円や双曲線)の交点のひとつとして解が得られることになる.p=4の場合,(1)-(2)=0は
(2-2x-2y)^2+2(2-2x-2y)+2y^2-(2-2x-2y)^2-2x^2=2(2-2x-2y)+2y^2-2x^2=0 (双曲線)
(2)-(3)=0は
(2-2x-2y)^2+2x^2-2x^2-2xy-2y^2=(2-2x-2y)^2-2xy-2y^2=0 (双曲線)
(3)-(1)=0は
(2-2x-2y)^2+2(2-2x-2y)+2y^2-2x^2-2xy-2y^2=(2-2x-2y)^2+2(2-2x-2y)=0 (双曲線)
となる.以下に,阪本ひろむ氏にお願いして描いてもらった図を掲げておく.
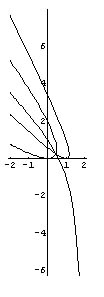
なお,p=3の場合
x=(3−√5)/2=0.381966
y=−2+√5=0.2362068
が得られたことを付記しておく.
===================================
【3】雑感
今回のコラムでは「ねじれ立方体」「ねじれ12面体」について取り上げました.この型の準正多面体にはねじれる方向によって右手系と左手系があります.
また,ミラーの多面体は小菱形立方八面体[3,4,4,4]の一方の八角鉢だけを45°回転させたものです.ねじれ立方体は正八面体群に属する立体図形であるのに対し,ミラーの多面体は正八面体群にはなりません.ミラーの多面体のねじれは切稜立方体の工程を一部変えることによってすでにできていますから,これですべての正多面体・準正多面体の木工模型が完成したことになります.

正多面体・準正多面体の木工製作可能性が確立したわけですが,次なるテーマとして経済性を求める問題<最小工程問題と最小余白問題>は未解決のままです.最小余白問題,すなわち,立方体あるいは直方体から多角形を作るときできるだけ余白を少なくし,できる限り大きな体積の多面体を作りたいというのはごく自然な発想でしょう.工夫次第ではいまある正四面体や正八面体よりももっと大きなものが作れるものと思われます.
また,ねじれ準正多面体では3次元定規を使わない工程とするために中間的に2p角形,6角形,4角形からなる多面体[4,6,2p]を作り,それを切って[3,3,3,3,p]を仕上げました.この着想は正解と思います.しかし,4角形面は最終的に1本の稜だけが残るだけです.したがって,4角形面を作る切稜プロセスは,ねじれ準正多面体を作りやすくするためのものであっても工程的には無駄なプロセスとなっていることがわかります.
このような無駄を省こうとする工夫が最小工程問題なのですが,適切な工程で行えば最小の費用(時間とコスト)の下で得られるべき立体の体積を最大にすることができるようになり作業能率は向上します.このような意味から,最小工程問題は最小余白問題と同時に取り組まれるべきものと考えられました.
===================================