今回のコラムでは，２次元骨組みを扱う．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　各頂点において力学的釣り合いが満たされなければならない．結論を先にいうと，ｖ頂点を抑え込むのに必要な最少の棒材数は

　　ｅ＝２ｖ−３

である．

　２次元では

　　ｅ≧２ｖ−３

によって，剛体か否かの判別が行われるのであるが，ｅ＝２ｖ−３を満たすにも関わらず剛体でない場合，棒材の組み替えによって，頂点の位置を動かさずに剛体に変換することができる．

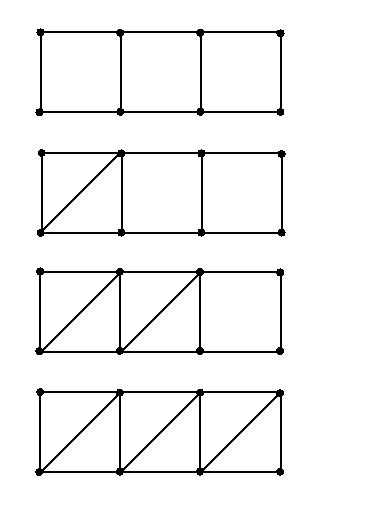
　１×３格子（ｖ＝８，ｅ＝１０）の場合の最少筋交い数は３である．すべての格子に筋交いを入れない限り剛性は保たれない．したがって，一番下の図だけが剛である．

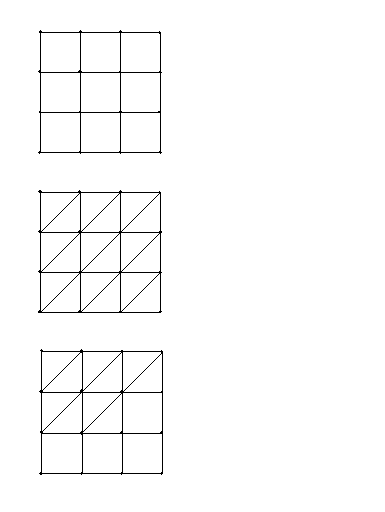
　３×３格子（ｖ＝１６，ｅ＝２４）の場合の最少筋交い数は５である．６や７では多すぎ（冗長）だが，４では少なすぎ，すなわち筋交いを５から１カ所取り除くだけで構造物の剛性が損なわれてしまう．また，一番下の図はｅ＝２ｖ−３を満たすにも関わらず剛体でない．

［Ｑ］一般に，ｎ×ｍ格子の最少筋交い数はいくつになるだろうか？

［Ａ］答えを先にいうと，最少筋交い数は

　　ｎ＋ｍ−１

であり，それを越える場合はいくつかの筋交いを削除することが常に可能である．以下にその証明を掲載する．

［証］２次元骨組みにおいて，ｖ頂点を抑え込むのに必要な最少の棒材数は

　　ｅ＝２ｖ−３

である．

　ｎ×ｍ格子の格子点数と辺数は

　　ｖ＝（ｎ＋１）（ｍ＋１）

　　ｅ＝ｎ（ｍ＋１）＋ｍ（ｎ＋１）

　したがって，不足している辺数は

　　２ｖ−３−ｅ＝ｎ＋ｍ−１

これを越える場合はいくつかの筋交いを削除することが常に可能である．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［Ｑ］ｎ×ｍ格子の筋交いをどこに配置すべきか？

［Ａ］格子の補強は完全２部グラフＫn,mのサブグラフとして表現することができる．そして，サブグラフが木である場合（回路を持たない場合）（かつその場合に限り）最少である．

　このグラフにおいて，頂点番号の付け替えは各行（または各列）の置換に対応する．対称性を考えると第１行（列）と第２行（列）の置換，第３行（列）と第２行（列）の置換，その組み合わせを行ってみると，剛なものは剛なものに，剛でないものは剛でないものに変換される．

［１］剛・剛変換

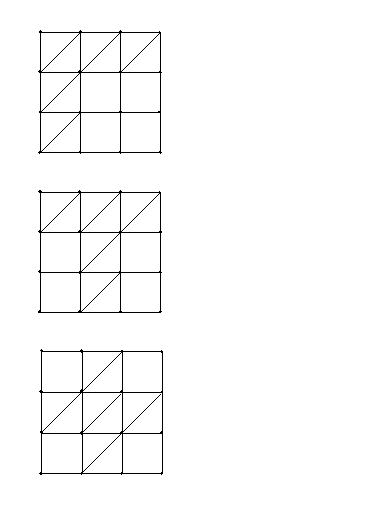
［２］不剛・不剛変換

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
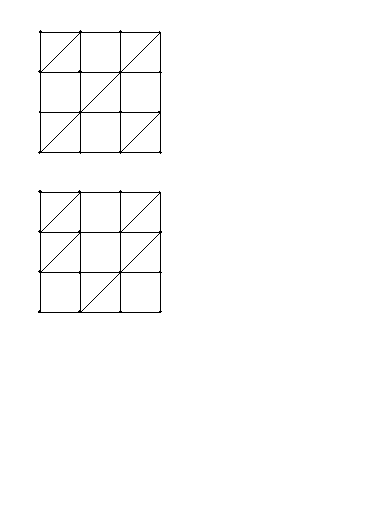