１：√３は正三角形の底辺の長さの１／２と高さの比である．白金比と呼ばれることもあるようだ．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　半径が等しく，その中心が互いの円周上にある２円が重なり合った共通部分のレンズ型（魚の形）の縦横比は１：√３になる．これはVesica Piscis（魚の膀胱？）として知られた神聖な形だそうであるが，膀胱はともかくとして確かに魚の形を想起させる．これは「ルーローの二角形」として知られた形でもある．

　ところで，正方形に内接しながら回転することができる円以外の図形は何かという問題の答えは「ルーローの三角形」としてよく知られている．ルーローの三角形は半径が等しく，その中心が互いの円周上にある３円が重なり合った共通部分である．

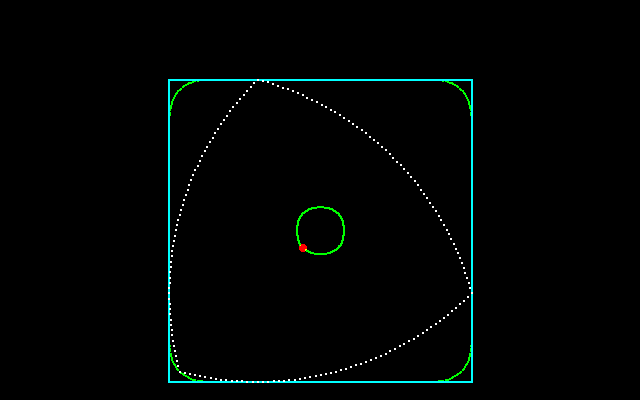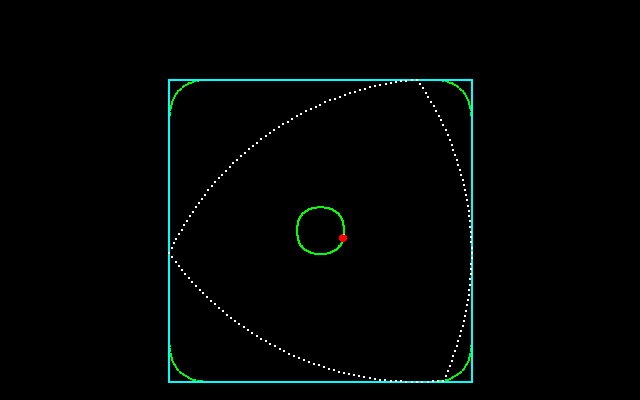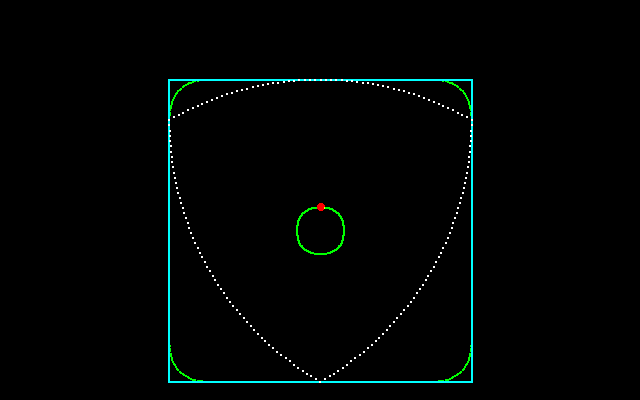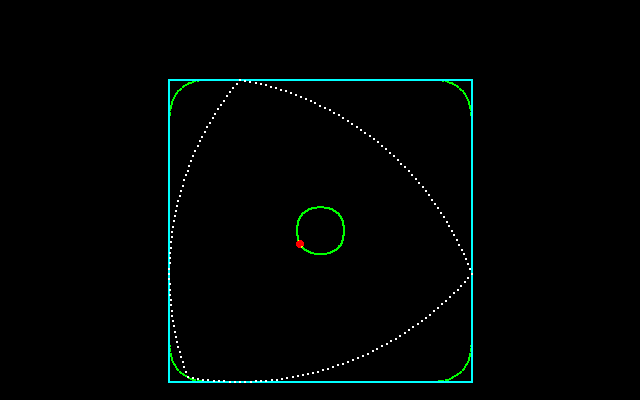
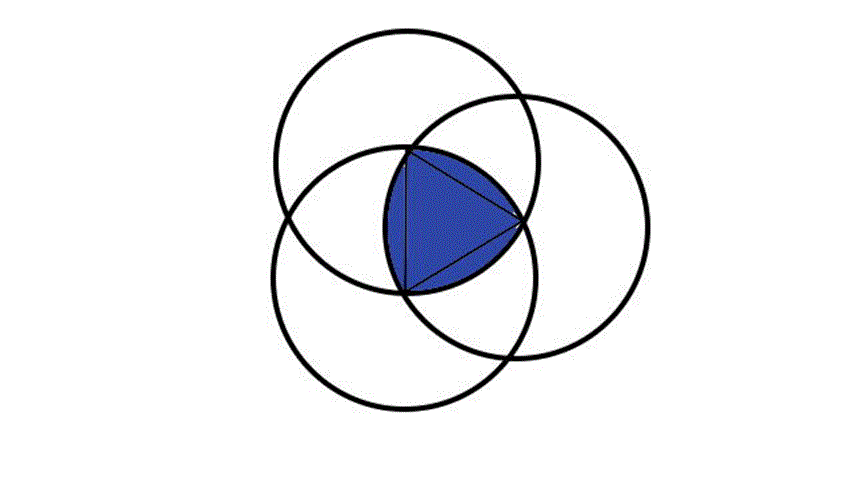
　それに対して，正三角形に内接しながら回転することができる円以外の図形は何かという問題の答えが「ルーローの二角形」である．ルーローの二角形は半径が等しく，その中心が互いの円周上にある３円が重なり合った共通部分である．

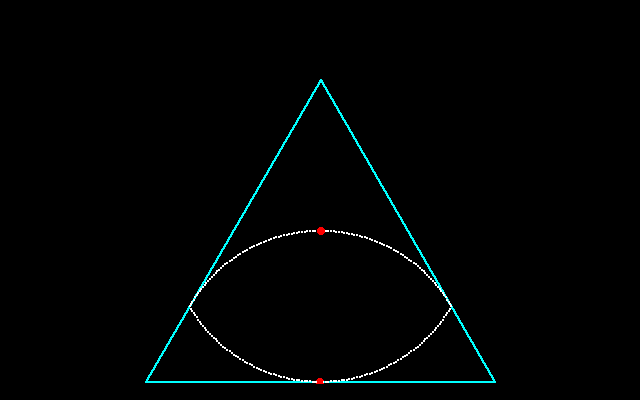
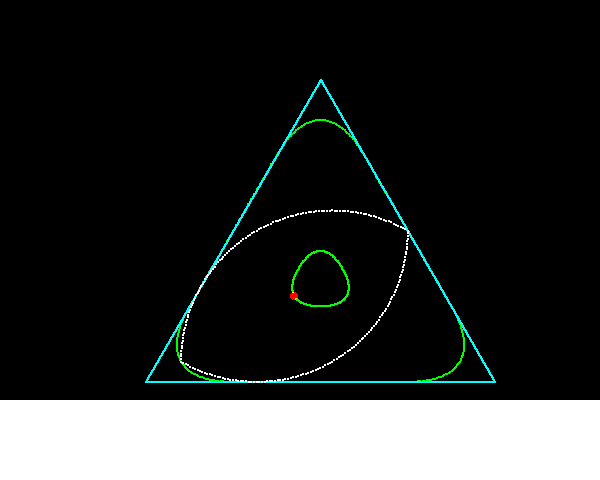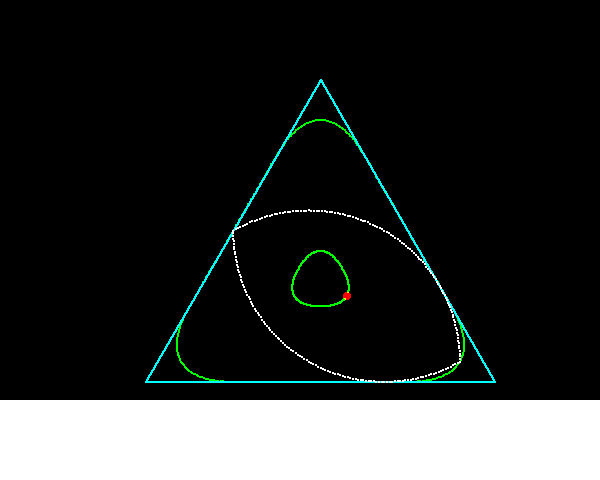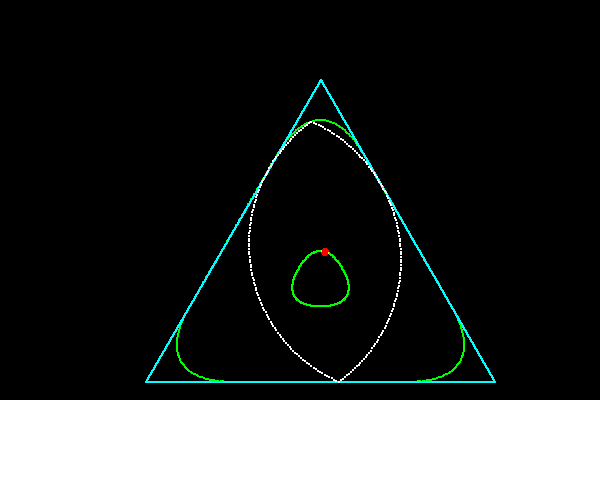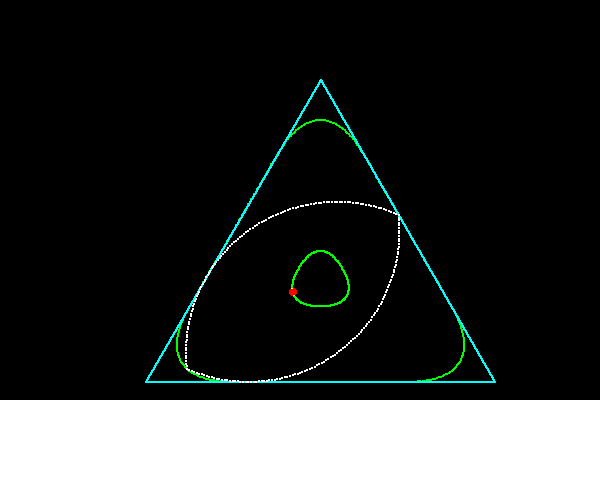
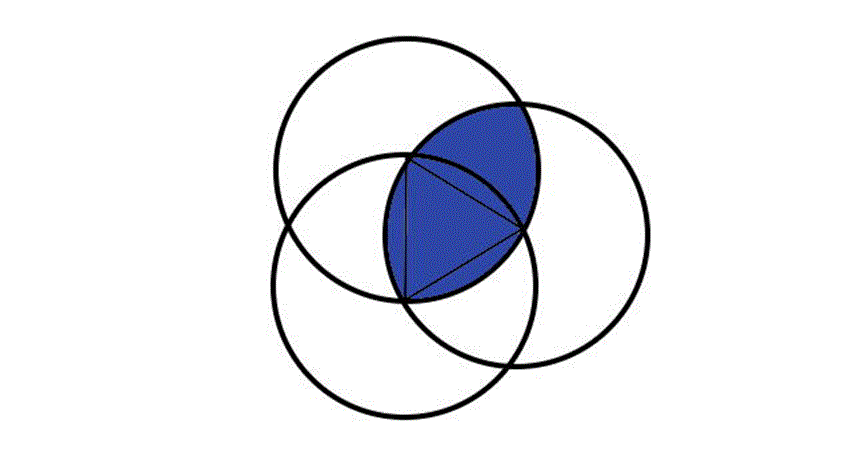
　なお，Vesica Piscisを用いた正五角形の近似的作図法が知られている．コンパスと定規を用いて，正六角形と組み合わせることで，許容内の精確さの正五角形が得られるそうである．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝