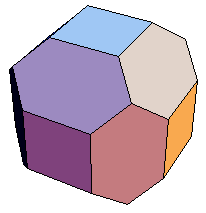
中川宏さんの切稜立方体(18面体)

については,最初はみたことのない立体ということで注目したのですが,切稜立方体を切頂八面体型に組み上げたランプを実際に手にすると,切稜立方体と立方体の2種類の立体による空間充填が可能であることが直ちに観てとれます.
そして小川泰先生のご指摘によりそれが菱形十二面体による空間充填の変形であることも理解できます.すなわち,
1)菱形十二面体には1つの頂点に3面が会するところと4面が会するところがある
2)4面が会する頂点を切頂して屋根型に切り取る
3)屋根(立方体を6分割した扁平な四角錐)が6個で立方体になる
というわけです.
面心立方格子の12個の球の中心を結べば立方八面体という準正多面体が得られますが,その双対すなわち面心立方格子のボロノイ多面体は対角線の長さの比が√2:1の菱形12枚で囲まれる菱形十二面体です.菱形十二面体は,面が正多角形ではないので準正多面体ではありませんが,空間充填形の1つとなっています.→[補]
===================================
【1】切稜立方体は球に外接する
(Q)中川さんよりの質問です.
「先日,18面体の面取りの深さによっては球に内接するかもしれないと書きましたが,あらためて18面体を六角形の面を正面にして輪郭を見て見ますと,六角形が三つ集まっているあたりの角度が面取りの深さを変えても決して球に接しないように感じました.いかがでしょうか?」
(A)正多面体は球に内接・外接しますが,準正多面体は球に内接するだけで外接しません.どちらも外接球を描くことができる,つまり,立体のすべての頂点が1つの球に接するようにできるわけですが,正多面体のすべての面に接するような内接球がただ1つ存在するのに対し,準正多面体ではかならず2〜3の内接球が必要になってしまいます.
それでは,切稜立方体ではどのようになっているのでしょうか? 投影した際の輪郭が正8角形になるような向き,すなわち,正方形面が手前を向くようにします.
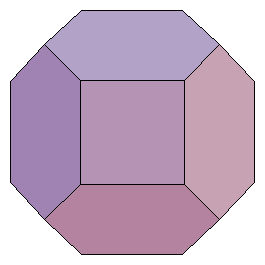
もとの立方体の1辺の長さを2,正方形面の1辺の長さをdとおくと,この図から
d=2(√2−1)
が得られます.これより,正方形面の頂点の座標は
(√2−1,√2−1,1)
の±を含めた巡回置換によって得られることがわかります.そして,原点から頂点までの距離の2乗は
2(√2−1)^2+1^2=7−4√2
一方,六角形面が三つ集まっている頂点の座標は
(1/√2,1/√2,1/√2)
ですから,原点からの距離の2乗は
3(1/√2)^2=3√2/2
で両者は一致しません.
このことから球に内接しないことがわかります.中川さんの予想の通りですが,切稜立方体はこの点においても準正多面体とは異なる立体ということになります.
次に,六角形面の中心までの距離を求めてみます.六角形面の中心の座標は
(1/√2,1/√2,0)
の巡回置換ですから,原点からの距離の2乗は
2(1/√2)^2=1
正方形面の中心までの距離の2乗も1ですから,切稜立方体は球に外接することがわかりました.立方体の性質が中川さんの切稜立方体に遺伝しているのです.
===================================
【2】切稜立方体のバリエーション
中川さんの切稜立方体では,18面体の面取りを深くして正方形を小さくしたり大きくしたりすることで,いろいろなバリエーションを作ることができます.辺の長さが同寸で正方形面と六角形面よりなる18面体もそのひとつです.
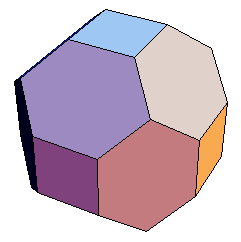
この場合について,同様の計算をすると
d=2(4√3−3)/13
となり,この立体は球に内接も外接もしないことがわかりました.
ここまでくると切稜立方体の一般的な外接・内接条件も求めたくなるというのが自然な成り行きです.球に内接するかどうかは18面体の各頂点と原点の距離を計算すれば答えは簡単にでます.また,外接するかどうかは面の中心と原点の距離を求めればよいことになります.
そこで,もとの立方体の1辺の長さを2,正方形面の1辺の長さをdとおくと,
正方形面の頂点の座標:(d/2,d/2,1)
六角形面の頂点の座標:(d/4+1/2,d/4+1/2,d/4+1/2)
六角形面の中心の座標:(d/4+1/2,d/4+1/2,0)
内接球が存在するための条件は
2(d/4+1/2)^2=1 → d^2+4d−4=0
を解いて
d=−2±2√2
0≦d≦2ですから
d=2(√2−1)
となり,中川さんの切稜立方体がこのケースにあたる唯一の切稜立方体であることがわかります.
また,外接球が存在するための条件は
2(d/2)^2+1=3(d/4+1/2)^2 → 5d^2−12d+4=0
d=2または2/5が解ですが,d=2はもとの立方体のままですからd=2/5が求める条件となります.
===================================
【3】切稜立方体による積み木
d=2(√2−1)・・・球に外接
d=2/5・・・・・・・球に内接
それ以外・・・・・・・・外接も内接もしない
ことがわかりました.
中川さんの解説によると
(1)積み木のように組み立てるという観点からすると,多面体のすべての面が球に外接しているということが重要で,頂点同士を繋ぐわけではないので球に内接する必要はかならずしもない.
(2)全体が切頭8面体(正方形6面,正6角形8面)の形状になっているもののほかに,正八角形6枚,正六角形8枚,正方形12枚でできる26面の準正多面体型(大菱形立方八面体)の積み木もできている.これには六角形の面同士だけでなく正方形の面同士を接合する箇所も含まれている.
(3)切稜の18面体は作りやすい割には組み立てに適した面数が多い「掘り出し物」だといえるかもしれない・・・
とのことでありました.
おっしゃるとおり球に外接することがいかに大切かがわかりますが,このことは中川宏さんの切稜立方体
d=2(√2−1)
が球に外接する唯一の切稜立方体であるという事実と整合しています.また,すべての辺が同寸の18面体は球に内接も外接もしないので積み木としては全く役に立たないものと思われました.
これらについては,頭のなかであれこれ考えていてもわかりにくいことなので,
山口県山口市 中井産業株式会社 中川宏
積み木インテリアギャラリー<http://ww6.enjoy.ne.jp/~hiro-4/>
を実際にご覧いただく方が近道だと思います.
===================================
【4】形の研究について思うこと
切稜立方体を組み上げた積み木は,小川泰先生をして「刺激的な作品」と言わしめました.そこにはもっと一般的な関係が潜んでいるかもしれませんし,小川先生であればそこから何か一般的なことを抽出してくださるような気がしています.
ところで,中川さんよりのメール
「木工会社の一介の工員の工作が学問研究のお役に立てるなんて感無量です.無学の者が勝手なことを申し上げてすみません.ただわたしはこの18面体工作をライフワークと任じておりまして,その意義を教えてくださる先生の見識にすこしでもついていきたいと念願しております.今後ともご指導のほどよろしくお願いいたします.」
が少し気にかかりました.
私は殊に形の研究に関しては専門の数学教育を受けたとかうけないとかはほとんど関係がない,形に対する熱意で充分だと思っていますが,読者のみなさんがこの意見に同意してくださるように,アマチュアにだって形の研究ができるという実例を紹介します.
それは平面充填型に関するものですが,正多角形による平面充填型には3種類(正三角形,正方形,正六角形)あります.正多角形でない多角形による平面充填形では,三角形と四角形の場合は凸でなくてもよいのですが,どんな形の三角形,四角形でも平面を過不足なく敷きつめることができます.凸六角形では本質的に異なる3つのタイプの六角形だけが平面を埋めつくします.また,凸な多角形では七角以上になるとどんな型のものもうまくいきません.
そこで,正多角形でない場合の平面充填では五角形のケースが特に重要になってきます.正五角形はどうしても隙間があいてしまいますが,凸五角形では,ホームベース形も含めて,現在,14種の平面充填形が知られています.六角形に関しては3種類以外のものは存在しないことが示されていますが,五角形に関しては14種ですべてかどうかはまだ証明されていません.
このような問題はとかくとり漏らしやすいもので,見逃されているものがあるやもしれません.1975年にはほとんど数学を学んだことのない主婦ライスが「サイエンティフィック・アメリカン」誌の記事に触発されて,五角形で平面を敷き詰めるパターンでそれまで知られていないものを3種類も発見したほどですから・・・.
数学に縁のない主婦がそれまで知られていなかった3種類の五角形の平面充填型を発見した・・・おそらくかなりの時間を費やした探求だったに違いないのですが,彼女の熱意の賜物であり,それに対する正当な報酬と考えることができると思います.プロの数学者だって熱意あるアマチュアに較べ,時間や道具立ての面でそれほど恵まれているとも思われません.
最後に,中川さんが切削したd=2/5の写真を掲げます.

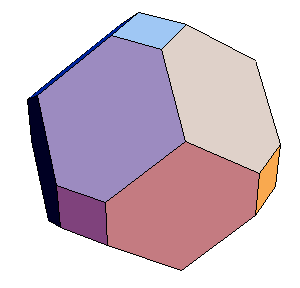
===================================
[補]3次元格子のボロノイ領域
まず,簡単な縄張りのモデルを考えてみましょう.草原のいくつかの巣穴にネズミが一匹ずつ棲んでいるとする.個々の縄張りが単独で存在するとき,縄張りはほぼ円であると考えることができますが,個体密度が次第に高くなってくると,縄張り所有者は互いに侵入者を追い払おうとしますから,縄張り間に境界が生じます.二匹のネズミの力に差がないとき,境界線は隣り合った2つの巣穴を結ぶ線分の垂直二等分線になり,そして,個体密度が十分高くなると,結局,棲息地はいくつかの凸多角形で分割されることになるのです.
このように,はじめに点の分布(母点)があって,隣り合った2点を結ぶ線分の垂直二等分線を次々に引いていくことによりできる多角形パターンは,ディリクレ領域またはボロノイ領域と呼ばれます.この概念は,はじめディリクレによって2次元で提出され(1850年),その後,ボロノイによって3次元に拡張されました(1908年).
研究分野によりいろいろな呼び名が使われていて,たとえば,地理学分野ではティーセン多角形と呼ばれていますし,物性物理学分野では,ウィグナー・ザイツセルという呼び名も用いられています.細胞(セル)の図と非常に似ているためでしょう.このように,ボロノイ分割は大勢の人が考えついて,しかも,いろいろな分野で独立に使われだしたようです.
ディリクレ領域の概念は3次元にも一般化できます(ボロノイ多面体).3次元格子には1848年にブラーベが発見した14種類あるのですが,これから決まる本質的なディリクレ領域は,ロシアの結晶学者フェドロフの見つけた5種類の平行多面体−−立方体,6角柱,菱形12面体,長菱形12面体(正6角形4枚と菱形8枚の2種類で作る12面体),切頂8面体−−しかありません.
平行多面体とは,平行移動するだけで3次元空間を埋めつくすことのできる単独の多面体であって,このうち,6角柱と菱形12面体は4次元立方体を3次元に投影したもの,長菱形12面体は5次元立方体を,切頂8面体は6次元立方体を3次元に投影したものと一致しています.
平行多面体は,結晶構造と深く関係していて,それぞれ,単純立方格子,六方格子,面心立方格子,底心格子(直方体の8個の頂点と上面・下面の面の中心に原子が配置されている構造),体心立方格子に対応するボロノイ領域です.これら5種類の平行多面体は,5種類の正多面体(プラトン立体)ほどよく知られていませんが,少なくとも同じ程度に重要であると考えられる所以です.
===================================