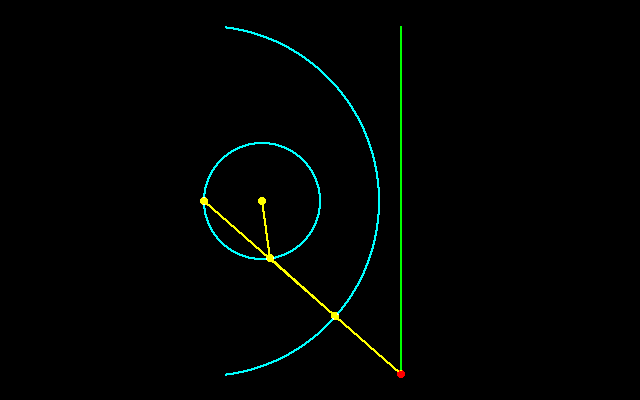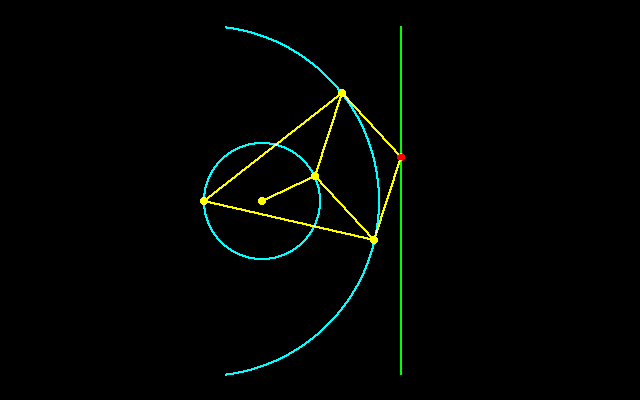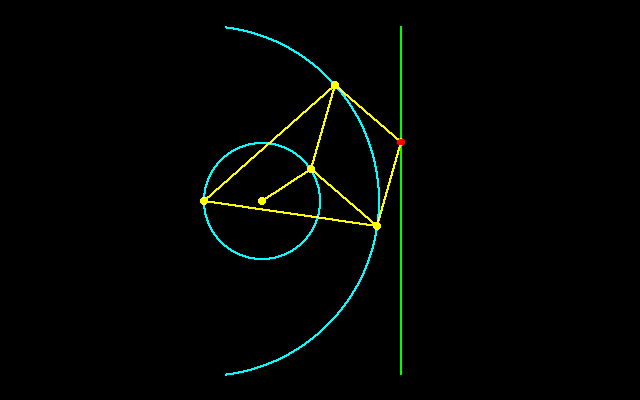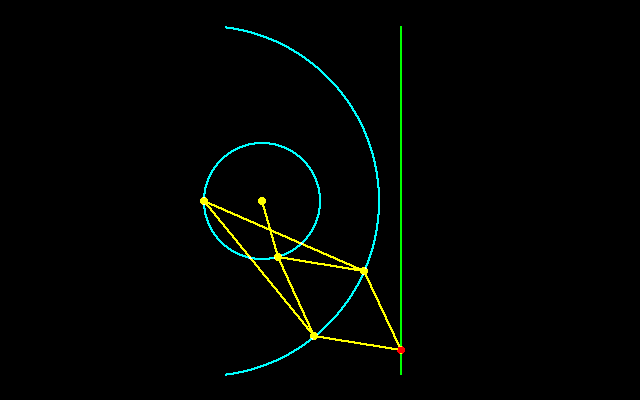
【１】ポースリエの反転器

　円運動を直線運動に変換することは水車や蒸気を動力とする産業革命の中心的な技術であるが，ワットの近似直線機構から８０年以上たった１８６４年，フランスのポースリエによって，精確に直線に沿って動くリンケージが考案された．ワットのリンケージは近似的な解にすぎなかったが，ポースリエの反転器は真正直線機構という機構学的問題のひとつの解答となった．彼はこの功績によりフランス学士院賞を受賞した．

　ポースリエの反転器は円運動を直線運動に，直線運動を円運動に変換する機構で，蒸気機関などに応用され，リンク装置の用途は多方面にわたっています．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】ケンペの万能定理

　リンク装置の一点を直線や曲線に沿って動かすとき，任意の（高次）代数曲線を描くことができる（ケンペの万能定理，１８７６年）・・・すなわち，尖点があってもかまわないし，いかに複雑な変化のある曲線でも描くことができます．あなたの名前をサインするリンク装置が存在するというわけです．

［補］すべての代数曲線はリンケージによって作図可能であることが示されたが，任意の連続曲線を描くことができるかどうかは未解決問題である．

［補］ケンペの証明（１８７６年）には欠陥があったが，証明の技術的な困難さは克服されず，２００２年になってカポヴィッチとミルソンにより完全に決着した．ケンペの職業は弁護士であったが，非常に優秀なアマチュア数学者でもあった．１８７９年には四色定理の不完全な証明をしたことで最も有名であるが，リンク装置にまつわる話もこれによく似ている．彼の証明は間違ってはいたが，全体的な考え方は非常に聡明なものであったという．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【３】サイクロイド

　固定した直線上を円が滑らずに転がるとき，回転円上の固定点のなす軌跡はサイクロイドと呼ばれ，回転円の半径をｒとすると

　　ｘ＝ｒ（θ−ｓｉｎθ），ｙ＝ｒ（１−ｃｏｓθ）

と書くことができます．

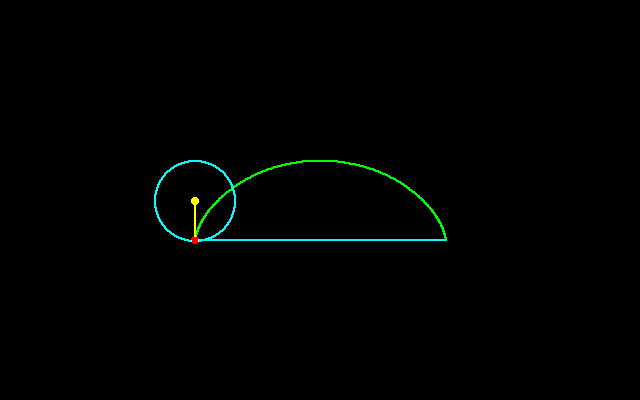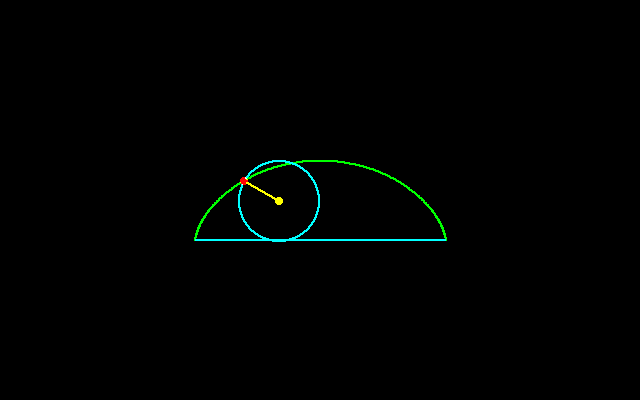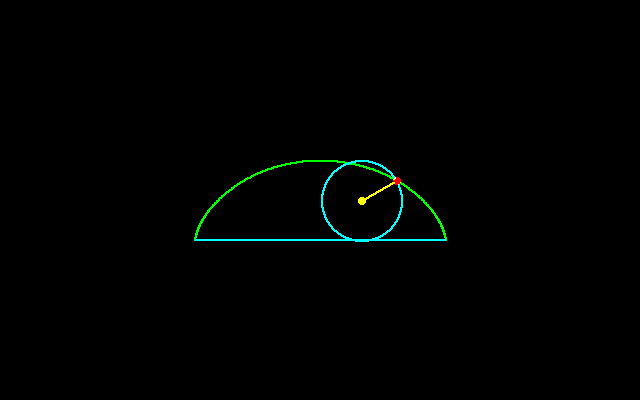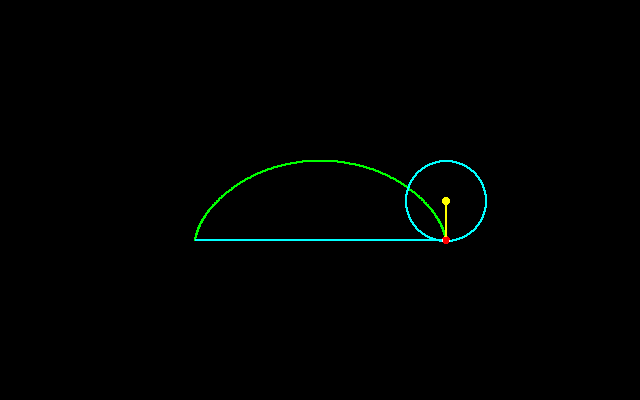
　この曲線は２変数多項式ｆ（ｘ，ｙ）＝０の形に表せませんから，代数曲線でありません．サイクロイドには

［１］最速降下線

［２］等時曲線

［３］縮閉線も伸開線もサイクロイドであること

など，いくつかの興味深い特性があります．

　サイクロイド：ｘ＝ｒ（θ−ｓｉｎθ），ｙ＝ｒ（１−ｃｏｓθ）の縮閉線は

　　ｘ＝ａ（θ＋ｓｉｎθ），ｙ＝−ａ（１−ｃｏｓθ）

です．ここで，θ＝π＋ｔとおけば

　　ｘ＝ａ（ｔ−ｓｉｎｔ）＋ａπ，ｙ＝ａ（１−ｃｏｓｔ）−２ａ

ですから，もとのサイクロイドと合同なサイクロイドになることが示されます．（なお，対数らせんの伸開線もそれと合同な対数らせんになる．）

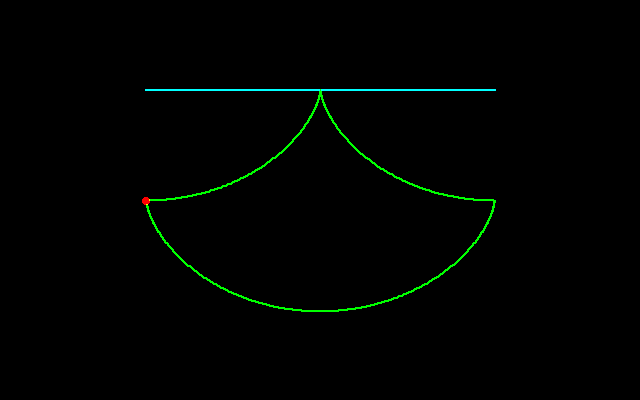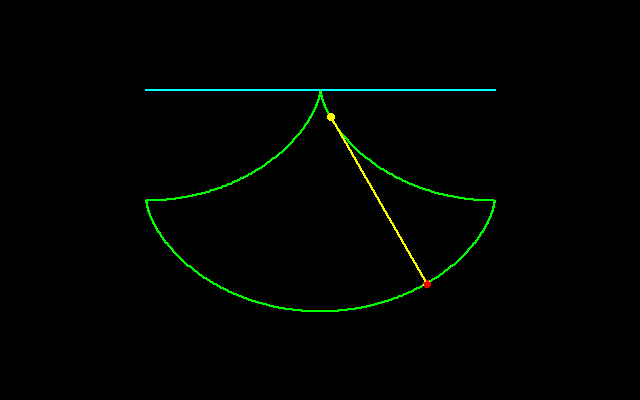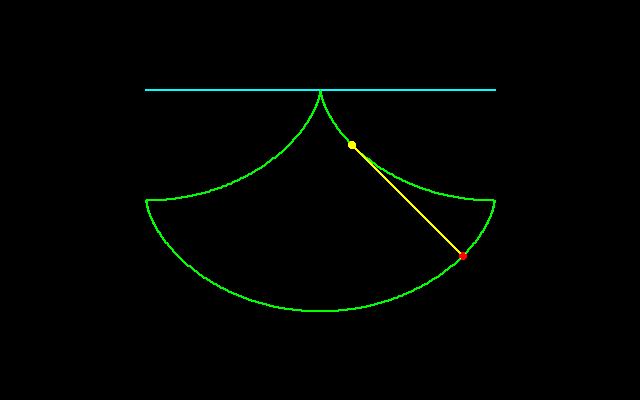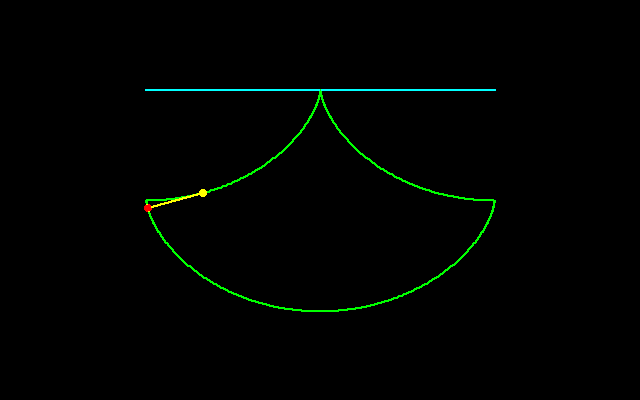
　サイクロイドはそもそもガリレイによって発見され，ホイヘンスによって振子時計の設計に使われ，そしてパスカルの積分法の研究にも貢献しています．サイクロイド弧が囲む面積は３πｒ^2（回転円の面積の３倍に等しい），弧長は８ｒ（回転円に外接する正方形の周に等しい）になります．

　なお，歯車の形となる曲線はサイクロイド（エピサイクロイドとハイポサイクロイド）とインボリュートです．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝