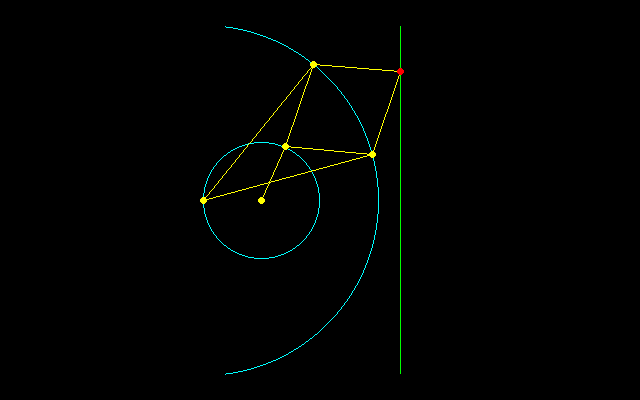
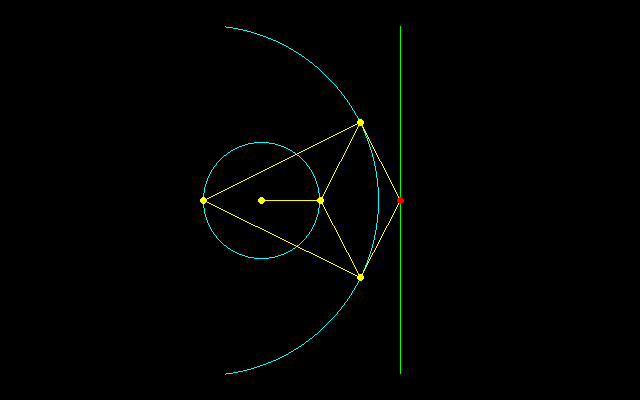
ポースリエの反転器は円運動を直線運動に，直線運動を円運動に変換する機構で，蒸気機関などに応用され，リンク装置の用途は多方面にわたっています．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】ポースリエの反転器

　円運動を直線運動に変換することは水車や蒸気を動力とする産業革命の中心的な技術であるが，ワットの近似直線機構から８０年以上たった１８６４年，フランスのポースリエによって，精確に直線に沿って動くリンケージが考案された．ワットのリンケージは近似的な解にすぎなかったが，ポースリエの反転器は真正直線機構という機構学的問題のひとつの解答となった．彼はこの功績によりフランス学士院賞を受賞した．

　ポースリエの反転器では菱形が対角線ＰＱに関して広がったり狭まったりする．この対角線の延長上には基点Ｏがあり，積ＯＰ・ＯＱが一定である．そのため，点Ｐが円周上を動くと点Ｑは直線上を動き，反転すなわち円を円（直線）に変換ことができる．

　大円の半径をＲ，小円の半径をｒ，菱形の１辺尾長さをＬとすると，基点Ｏと直線間の距離は

　　（Ｒ^2−Ｌ^2）／２ｒ

である．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

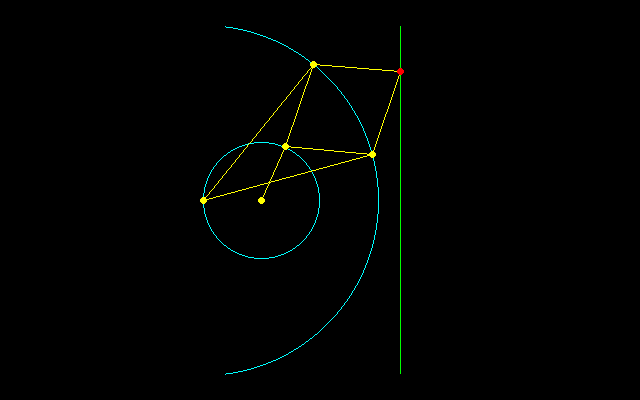
【２】ハートの反転器

　リンク数は多くなると機械として実質的に動かなくなるので，リンク数の少ない単純な仕組みが望まれる．ポースリエの反転器が７リンクであるのに対して，１８７５年，ハートは５リンクから構成される直線運動メカニズムを構成した．これ以上（４本）リンク数を少なくすることはできない．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【３】反転（円円対応と等角変換）

　ユークリッド平面の反転ではまず定点Ｏを中心とする半径ｒの定円を考えます．点Ｐに対して直線ＯＰ上に

　　ＯＰ・ＯＱ＝ｒ^2

となる点Ｑをとる写像を円Ｏに対する反転といいます．

　平面の反転によって円の内部の点は外部に移り，周上の点はその点自身に，外部の点は内部に移ることは明らかですが，

　(1)点Ｏを通らない円は，Ｏを通らない円に移る

　(2)点Ｏを通る円は，Ｏを通らない直線に移る

　(3)点Ｏを通る直線は，それ自身に移る

　直線および円は直線または円になるというわけですが，直線も半径が無限大の円と考えることができますから，反転の特徴は「円は円に変換される」ということができます．

　空間の反転では円，直線をそれぞれ球面，平面に読みかえればよいので

　(1)点Ｏを通らない球は，Ｏを通らない球に移る

　(2)点Ｏを通る球は，Ｏを通らない平面に移る

　(3)点Ｏを通る平面は，それ自身に移る

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

　反転のもう一つの特徴は２曲線のなす角を変化させない「等角写像」であるということです．反転操作は最も簡単な等角変換ですが，多くの等角写像があり，たとえば，球面上の定点Ｏから球面上の任意の点ＰをＯを一端とする直径に垂直な平面に移す極投影も等角変換のひとつとなっています．

　１次分数変換（メビウス変換）

　　ｗ＝ｆ（ｚ）＝（ａｚ＋ｂ）／（ｃｚ＋ｄ）

は複素数球面上で考えると１つの回転に対応していて，たとえば，数ｚを

　　（ｚ−１）／（ｚ＋１）

に置き換えるには，北極と南極が赤道のところにくるように球を９０°回転させればよいのですが，この写像は等角写像になります．

　等角変換は円は円に移り，直線も円へ移るという性質を併せもつというわけです．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【４】反転の応用

　接する円の族に関する定理では何百という美しい定理があるが，シュタイナー円鎖について述べておきたい．小円を大円の内部におき，この２つの円の中間に次々に接する円列を作る．たいていの場合，最後の円は重なってしまい，この円列は互いに接する円環をなさない．しかしときとして完全な円環をなす場合がある．これがシュタイナー円鎖である．

　最も簡単なものとしては，たとえば，半径が３と１の同心円に対しては６個の単位円よりなるシュタイナー円鎖が存在し，円の中心の軌跡は半径２の円となる（円の最密充填）．

　シュタイナー円鎖をなす円の中心の軌跡は楕円となる．アルキメデスのアルベロス（靴屋のナイフ）円列はシュタイナーの円鎖の特別な場合になっていて，円の中心はすべて基線上に長径をもつ楕円の上にのっている．

　ソディー（アイソトープの発見でノーベル賞を受賞した英国の化学者）の６球連鎖はシュタイナー円鎖の３次元版であるが，シュタイナー円鎖の場合とは異なって，球連鎖は常に繋がり必ず６個の球からなる．そして６個の球の中心，球同士の接点はすべて同一平面上にあるのである．

　反転によって，接する２円は接する２円か，円とその接線か，平行な２直線のいずれかにに移る．また，平面上の交わらない２つの円を同心円に移す写像が存在する．シュタイナーやソディーの定理はこれらの事実に基づいて証明されるのである．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【５】２つの定理

［１］シュタイナーの定理

　小円を大円の内部におき，この２つの円の中間に次々に接する円列を作る．たいていの場合，最後の円は重なってしまい，この円列は互いに接する円環をなさない．しかしときとして完全な円環をなす場合がある．このとき，最初の円をどこに選ぼうとも完全な円環をなす．

［２］ポンスレーの定理

　小円を大円の内部におく．大円上の点Ｐ0から小円へ接線を引き，大円と交わる点をＰ1とする．Ｐ1から再び小円へ接線を引き，大円と交わる点をＰ2とする．この２つの円の中間に次々に接する接線列を作る．たいていの場合，最後の交点は最初の点Ｐ0と重ならない．しかしときとして完全に重なる場合がある．このとき，最初の点Ｐ0をどこに選ぼうとも完全な多角形環をなす．

　２つの定理に共通する特徴は２つの円が同心円ならば自明であるということである．シュタイナーの定理はメビウス変換により同心円の場合に帰着させて証明できるが，ポンスレーの定理ではそれができない．

　ポンスレーの定理の場合，直線を直線に移す円板の変換が必要になるが，それは

　　ｘ’＝（ａｘ＋ｂｙ＋ｃ）／（ｕｘ＋ｖｙ＋ｗ）

　　ｙ’＝（ｄｘ＋ｅｙ＋ｆ）／（ｕｘ＋ｖｙ＋ｗ）

という形の（実）変換である．また，ポンスレーの定理は２つの円を２つの楕円の置き換えても成立する．

　ポンスレーの定理においてｎ＝３の場合，一方の円（半径Ｒ）に内接し，もう一方の円（半径ｒ）に外接する三角形は無数にある．これが成り立つための条件は２つの円の中心間距離をｄとして，

　　Ｒ^2−２Ｒｒ＝ｄ^2

となることである（オイラーの定理）．

　四角形やそれ以上のｎ角形についても同様の定理が成り立ち，ひとつの円に内接し，他の円に外接する四（ｎ）角形は無数にある．オイラーの定理のｎ角形版として，フースの定理が知られている．たとえば，内接円と外接円の両方をもつ四角形（双心四角形）では，

　　２ｒ^2（Ｒ^2＋ｄ^2）＝（Ｒ^2−ｄ^2）^2 　　　（フースの定理）

が成り立つ．フースは双心五角形，六角形，七角形，八角形に関する同様の公式も見つけている．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝