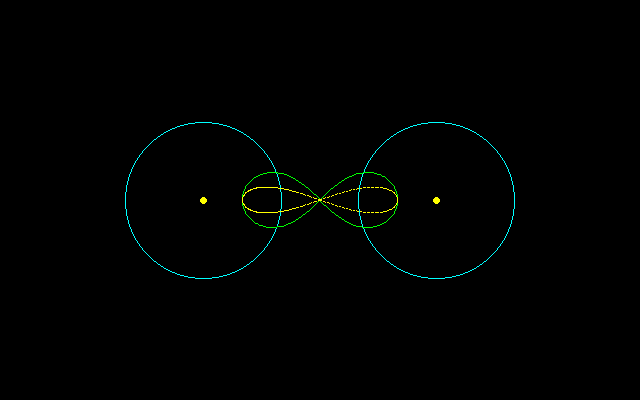
蒸気エンジンのピストンロッドを動かすためには，中点はほぼ直線上を動いた方が都合がいい．そのためには，ワットのリンク装置（リンケージ）が描く曲線はベルヌーイのレムニスケートではないほうがよいことに気づいた．

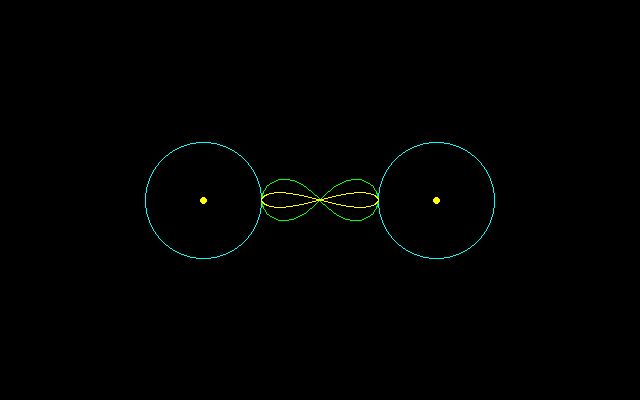
　ベルヌーイのレムニスケートではＲ＝ａ√２であったが，そのためには２Ｒ＜２ａとして左右の回転軸を逆向きに動かせば中点は概ねその間のバランスのとれたところにとどまり，ほぼ直線の長い部分をもつ８の字型曲線に沿って描くことになる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】ゲロンのレムニスケート

　ゲロンはフランスの数学者．Geronoのレムニスケート：

　　（ｘ，ｙ）＝（ｃｏｓθ，ｓｉｎθｃｏｓθ）＝（ｃｏｓθ，ｓｉｎ２θ／２）

はベルヌーイのレムニスケートより長い直線部分をもつ８の字型曲線である．

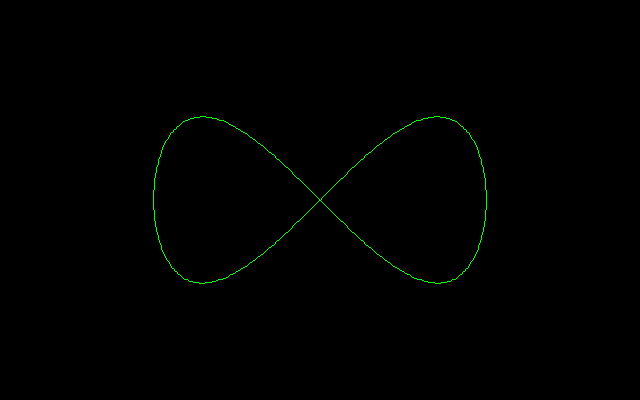
　ゲロンのレムニスケートはリサージュ曲線の１つとして知られている．すなわち，

　　ｘ＝Ａｓｉｎ（ω1ｔ＋φ1）

　　ｙ＝Ｂｓｉｎ（ω2ｔ＋φ2）

において，

　　Ｂ＝Ａ／２，ω2＝２ω1，φ1＝π/2，φ2＝０

とおけばよい．したがって，ワットのリンク装置（リンケージ）が描く曲線ではないことになる．

　なお，ゲロンのレムニスケート：ｙ^2＝ｘ^2−ｘ^4も

　　ｘ＝ｓｉｎθ＝（１−ｔ^2）／（１＋ｔ^2）

　　ｙ＝ｓｉｎθｃｏｓθ＝２ｔ（１−ｔ^2）／（１＋ｔ^2）^2

とパラメトライズされるから，ベルヌーイのレムニスケート：（ｘ^2＋ｙ^2）^2＝（ｘ^2−ｙ^2）もゲロンのレムニスケート：ｙ^2＝ｘ^2−ｘ^4も有理曲線というわけである．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝