【１】ベルトランのパラドックス

（Ｑ）中心Ｏ，半径ｒの円の内部に任意の点Ｐをとるとき，

　　ＯＰ＜ｒ／２

である確率はいくらか？

（Ａ１）中心Ｏ，半径ｒ／２の円の内部であるから１／４

（Ａ２）点Ｐは半径上の点であるから１／２

（Ａ３）点Ｐは半径を直径とする半円周上の点であるから１／３

　このように色々の解が考えられるが，こられ３つの解はどれも一応もっともである．ひとつの問題に対して幾通りもの違った解が導かれるのは驚きであって，ベルトランのパラドックスと呼ばれている．なぜ違った答えがでてきたのか，それは点分布のランダムネスの考え方の違いに基づいていることは明らかであろう．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

（Ａ１）円の中心から下ろした垂線の足が，円の内部に一様分布する．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

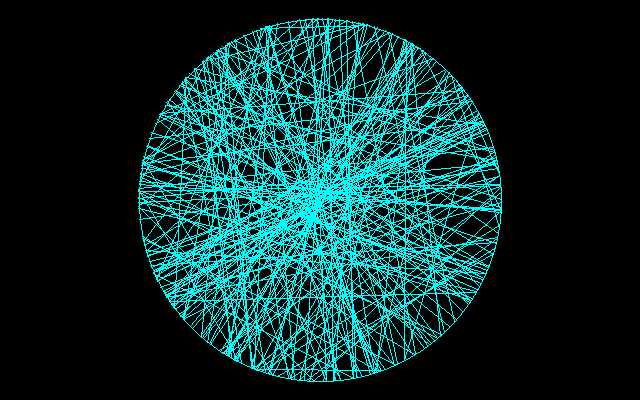
（Ａ２）円のひとつの直径上で一様分布し，直線の方向はこれとは独立に一様分布する．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

（Ａ３）２点が円周上で一様分布する．

　それぞれの測度に基づいて，２００本の直線を描いてみると（Ａ２）では直線が円内にまんべんなく分布しているのに対して，（Ａ１）（Ａ３）では直線の分布が円周付近に偏る傾向がみられる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】ボックス・ミューラーの正規乱数発生法

　ｘ1，ｘ2を標準正規分布にしたがう変数とすると，

　　exp(-1/2(x1^2+x2^2))

　　1/2πarctan(x1/x2)

は区間(0,1)の一様分布に従います．ここで，極座標変換x1=rsinθ,x2=rcosθすると

　　u1=exp(-r^2/2)

　　u2=θ/2π

も区間(0,1)の一様分布に従います．

　正規乱数を発生させる方法に，ボックス・ミューラー（Box-Muller）法があります．r^2=-2logu1,θ=2πu2ですから，２個の一様乱数ｒ1，ｒ2から互いに独立に標準正規分布に従う２個の正規乱数

　　ｚ1＝（−２ｌｎｒ1 ）^1/2ｃｏｓ（２πｒ2）

　　ｚ2＝（−２ｌｎｒ1 ）^1/2ｓｉｎ（２πｒ2）

を作りだすことができます．

　これがボックス・ミューラー法ですが，正規乱数発生法としては中心極限定理を利用する方法も知られています．中心極限定理による正規乱数発生法は，１２個の一様乱数から１個の正規乱数が得られる効率のよくない方法であったのに対し，ボックス・ミューラー法はかなり効率がよくなっています．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝