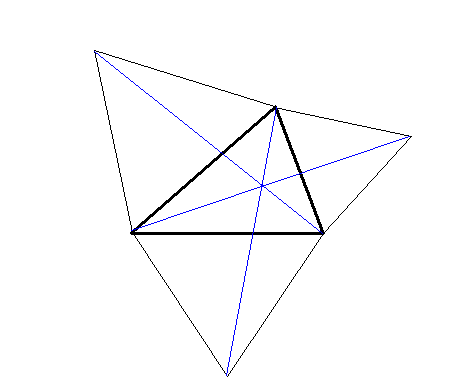
今朝，中川宏さんから「この心はなんと呼ばれていますか？」というメールがあった．各辺に正三角形たてて，その頂点と対角を結ぶ直線の交点である．

　以下，Ｓ（佐藤）とＮ（中川）のやりとり．

Ｓ：フェルマー点．１２０°で交わります．一松信先生のお話では三角形の心は１００ほどあるそうです．詳しい本としては

　　一松信「初等幾何入門」岩波書店

　　イボンヌ＆ルネ・ソルテ「なぜ初等幾何は美しいか」東京出版

Ｎ：ウェルズ「不思議おもしろ幾何学事典」朝倉書店にもありました．［１］１２０°，［２］同長，［３］最短距離．美しいですね．どうして学校では教えないのでしょう．

Ｎ：ところで，フェルマー点という名からすると１７世紀に発見されたようですが，あまりのも素朴な作図なので，このように１点に集まる心が存在することは昔から知られていたのではないでしょうか？

Ｓ：三角形の５心とは内心，傍心，重心，外心，垂心を指しますが，古代ギリシャ人は５心について知っていました．その１５００年後，フェルマー点が発見され，さらに１〜２世紀後に９点円の中心，その次がジェルゴンヌ点，１９世紀にはいるとナーゲル点やブロカール点などが発見されました．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】三角形の５心（はじめに三角形ありき）

　三角形の５心とは内心，傍心，重心，外心，垂心を指しますが，内心は内角の２等分線，傍心は１内角と２外角の２等分線，重心は中線，外心は辺の垂直２等分線，垂心は頂点から対辺への垂線が１点に会した共点です．

　このうち，三角形の内心は３辺への距離のうちで一番小さいものが最大となる点（マックスミニ点），外心は３頂点に至る最大距離が最小となる点（ミニマックス点）です．同様に，垂心は三角形に内接する三角形の周長が最小になる点，重心は３頂点に至る距離の２乗の和が最小となる点です．

　幾何学の基本形である三角形の性質について，もう一度見直してみることにしましょう．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】フェルマー点

　微分積分の入門書に「平面上に３つの定点Ａ，Ｂ，Ｃがある．この平面上に点Ｐをとって，ＡＰ^2＋ＢＰ^2＋ＣＰ^2が最小になるようにせよ」という問題が偏導関数の応用例として載せられています．その点Ｐは重心です．３定点が４定点であっても，同じ議論になるのですが，距離の２乗の和に特に具体的な意味があるようには思えません．むしろ，２乗を取り去ったほうが問題としては自然です．

　そこで，「Ａ，Ｂ，Ｃ３軒の家に電線をひきたい．電線の長さを最小にするにはどこの柱を立てればよいか」ではＡＰ＋ＢＰ＋ＣＰを最小にする実用価値のある問題になります．

　この問題は１７世紀のフランスの数学者フェルマーがイタリアの物理学者トリチェリ，数学者カヴァリエリに出題したものとして有名な問題で，求める点Ｐをフェルマー点といいます．点Ｐは三角形ＡＢＣの内部にありますが，∠Ａ，∠Ｂ，∠Ｃ＜１２０°のときには，３頂点に至る距離の和が最小となる点は３辺を等角１２０°に見込む点です．∠Ａ，∠Ｂ，∠Ｃのいずれかが≧１２０°のときには，それぞれ頂点Ａ，頂点Ｂ，頂点Ｃになります．

　このフェルマー点は頂点と外正三角形の頂点を結ぶ直線の共点として得られます．すなわち，フェルマー点を見つけるには与えられた三角形の各辺の上に正三角形を立てて各頂点と結ぶと，これら３本の線は１点Ｆで交わり∠ＡＦＢ＝∠ＢＦＣ＝∠ＣＦＡが成り立ちます．また，フェルマー点は３つの正三角形の外接円の交点でもあります．

　このような最短配線問題は最小木問題（問題の発案者シュタイナーに因んで最小シュタイナー木問題）と呼ばれていますが，ＶＬＳＩ回路を設計するときの最も基本的な技術となっています．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【３】９点円の中心

　外心と重心の中点はフォイエルバッハの９点円の中心であり，フォイエルバッハの９点円は各辺の中点，各頂点から対辺へ下ろした垂線の足，頂点と垂心の中点の９個の点を通る円となっています（１８２１年：ポンスレとブリアンション）．

　このことから，オイラー線（１７６７年）は外心・重心・垂心・フォイエルバッハの９点円の中心を相互に結ぶ直線ということになりますし，フォイエルバッハの９点円の中心はオイラー線の中点で，その半径は外接円の半径の半分となります．

　さらに，フォイエルバッハの９点円が三角形の内接円と傍接円の各々に接する，９点円には他にも多くの特別な点が含まれているなど，三角形のような簡単な図形が無数に未知の性質を有することはまことに不思議なことです．

　　［参］前原濶，桑田孝泰「知っておきたい幾何の定理」共立出版

に９点が同一円周上の存在することのエレガントな証明が掲げられています．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝