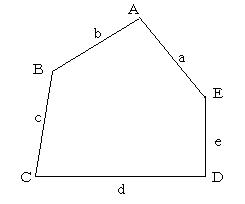
凸五角形によるタイル貼りの新しいタイプを４つも発見されたアメリカのマジョリー・ライスさんの真似をして、彼女が使ったであろう型紙をあれこれ並べ替えているうちに、既存の１４種類のタイプ表には見当たらないパターンがいくつか見つかった。

　まずその１は、

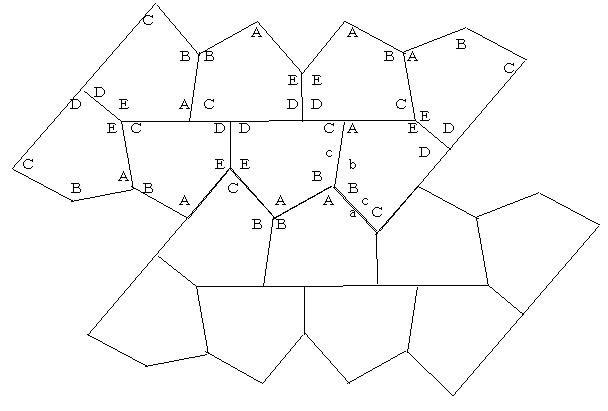
　上の図のように、正図と反転図それぞれ４枚ずつ、合計８枚で平行移動の基本単位をなす。充填条件は、角度について、

　２Ｄ＝１８０度、つまりＤ＝９０度

　Ａ＋Ｃ＝１８０度

　Ａ＋２Ｂ＝３６０度

　Ｃ＋２Ｅ＝３６０度

上の図では、Ａ＝１００度、Ｂ＝１３０度、Ｃ＝８０度、Ｄ＝９０度、Ｅ＝１４０度で描いてある。辺長については、

　ａ＝ｃ，ｂ＝ｃ　したがってａ＝ｂ＝ｃ

である。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　形の科学会で長年小川泰先生とともに系統的に凸五角形タイル張りの研究をされている杉本晃久さん（ISTA）にこれを検討していただいた。つぎの図はライスさんの手書きのスケッチを集めたものだそうだ。

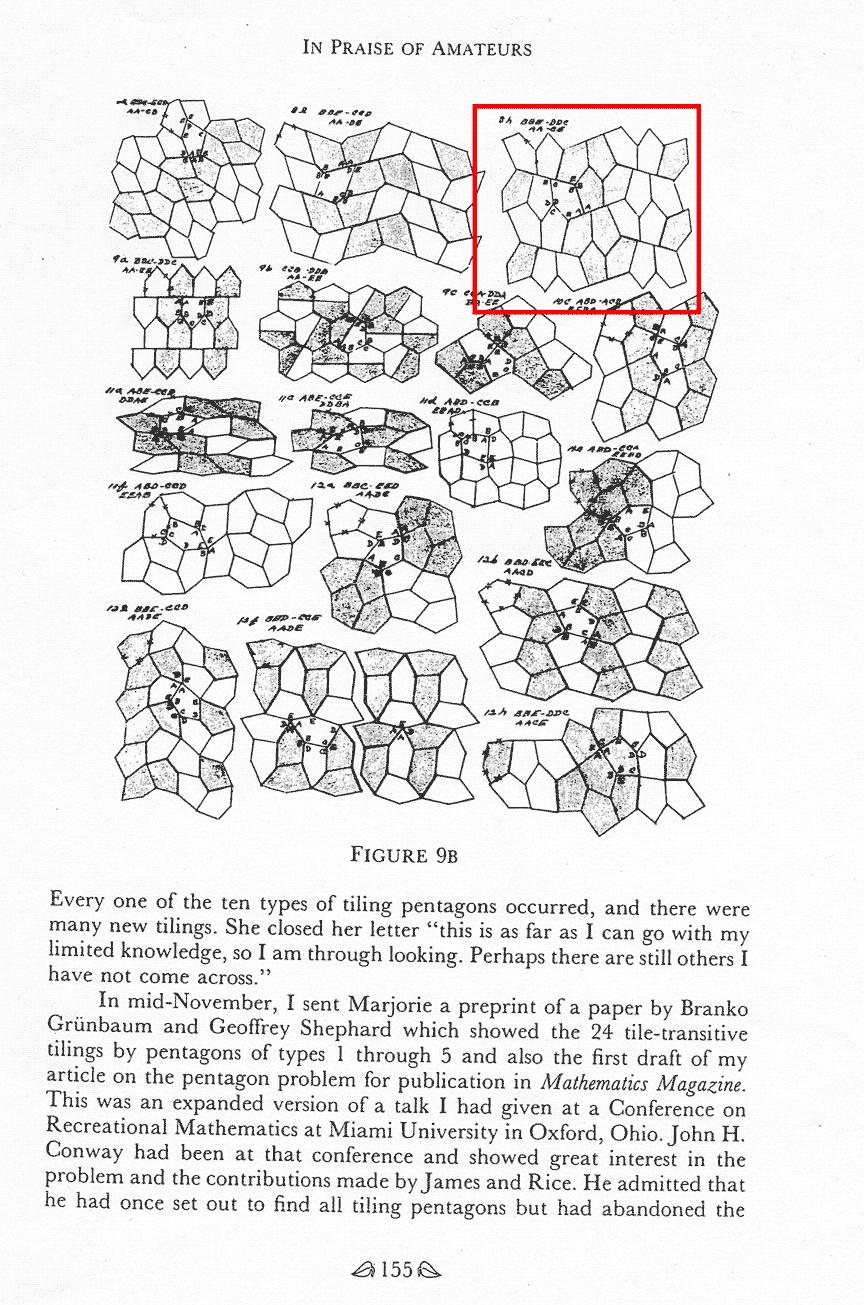
　赤枠で囲まれた図に注目されたい。一個一個の五角形の姿が若干違うことはともかく、ライスさんのスケッチでは８枚からなる基本領域が明示されていない（７枚までしか図の範囲では確認できない）ので？？という印象は免れないが、よくよく見ると確かに並び方は同じである。つまり、このパターンはライスさんが既に発見されていたものだということだ。ひょっとするとライスさんが見落としていたのかもしれないなどと浅はかにも思っていた私は、改めてライスさんの偉大さに敬服した次第である。

　さて、あきらかに既存のタイプ表にはない並び方をしているにもかかわらず、あたらしいタイプとして登録されなかったということはライスさんが発見した当時すでに、これが既存のタイプに属すると評価されていたことを意味する。じつはこの作業が素人には容易ではない。そこを杉本さんが解決してくださった。

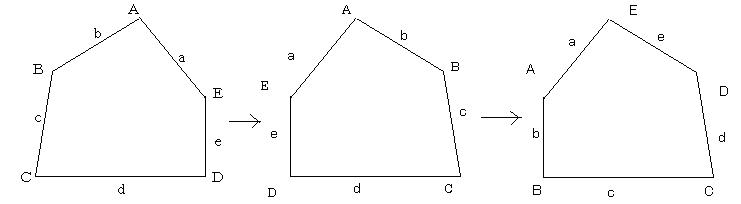
　私が記号をつけた左図をまず反転させると真ん中の図になる。さらに一番上に位置する頂点をＥとして反時計回りに記号をふりなおす。すると右のようになる。このように記号をつけかえた五角形を４枚１組で並べると次のようにタイプ２として知られているパターンに並べることができるというのだ。

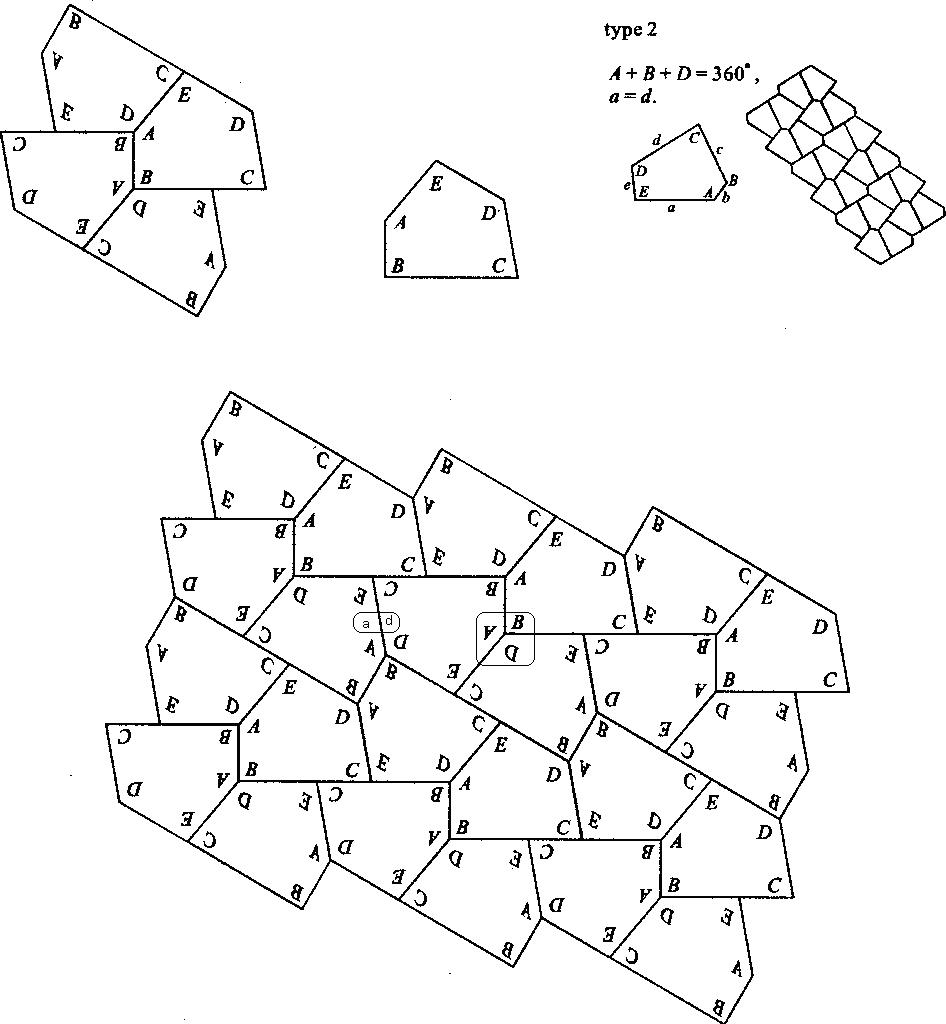
　言い換えると、タイプ２として知られている４枚１組のパターンをなす五角形の条件は

　Ａ＋Ｂ＋Ｄ＝３６０度

　ａ＝ｄ

であるが、これに以下の付加条件

２Ｂ＝１８０度、つまりＢ＝９０度

　Ｅ＋２Ｄ＝３６０度

　Ｃ＋２Ａ＝３６０度

　ａ＝ｄ＝ｅ

を課すと、８枚１組の別のパターンが生み出せるということである。　　　（中川宏）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝