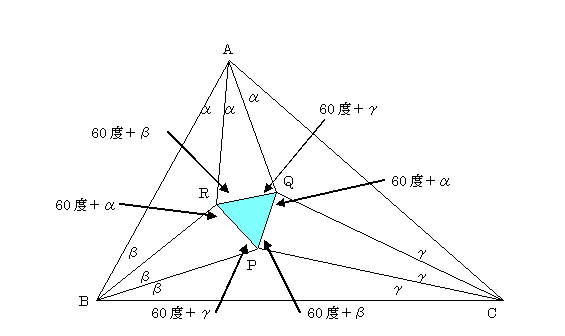
「任意の三角形の角の三等分線を描くと,隣り合う三等分線が交わる3つの交点は正三角形になる.」・・・これをモーレーの三角形と呼ぶが,モーレーの三角形が1899年,わずか100年前に発見されたというのは驚きである.
ところで,
[Q]モーレーの三角形の中心(重心)はもとの三角形の何と一致するのだろうかという問題に対しては,既知の諸心のどれでもなく(残念な結果であるが)「モーリーの正三角形の中心点」といわざるを得ないようである.今回のコラムでは,このことに関する一松信先生の計算結果とそういわざるをえない根拠も記したいと思う.
===================================
【1】三角形の有理的心(rational center)
三角形の有理的心とは,次のように表される点です.ある関数f(a;b,c)があり,巡回的にf(b;c,a),f(c;a,b)と表される.ここでfは
[1]a,b,cについての同次式
[2]f(a;b,c)はaを主変数とし,b,cについて対称
[3]a,b,cについての有理式(分母を払えば多項式)で表される
[1][2]は不可欠,[3]がある種の理論に必要で専らこの場合にしか扱わない場合もあります.有理的でないの心の一例は和心(Soddy点:AP+BC=BP+CA=CP+ABを満たす点P)で,その重心座標には平方根が入ります(内接円の半径が関与するので面積を表すヘロンの公式関連で平方根が入る)
それでも大半は定規とコンパスで作図できる点(和心もそう)に限っているので,モーリー三角形の中心点は異質です.
===================================
【2】モーリー三角形の中心点
モーリーの定理そのものの証明もいろいろあり,便宜上,3内角の1/3を∠A/3=α,∠B/3=β,C/3=γ (α+β+γ+60°)と記すと,小正三角形の一辺の長さは8Rsinαsinβsinγ (Rは外接円の半径であることが示されます.

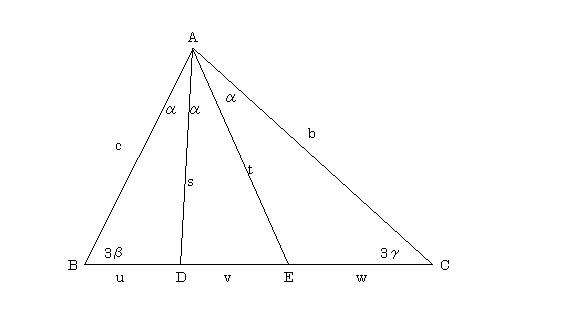
以下,3頂点の重心座標を計算します.その中心は(正規化した)P,Q,Rの重心座標の相加平均として表されます.そのための補助として∠Aを三等分した直線が対辺BCと交わる点をD,Eとし,
BD=u,DE=v,EC=W (u+v+w=a)
AD=s,AE=t
とおき,これらをa,b,c,α,β,γで表すことを考えます.
条件式は,u:v=c:t、v:w=s:b
正弦定理より,u/sinβ=s/sin3β
(v+w)/sin2α=(a−u)/sin2α=s/sin3γ
これから
a=(a−u)+u=(sinα/sinB)s+(sin2α/sinC)s (B=3β,C=3γ)
したがって,
s×(sinαsinC+sin2αsinB)=a×sinBsinC
≡abc/4R^2=S/R (SはΔABCの面積,Rは外接円の半径)
これから
s/2・(csinα+bsin2α)=S
s=2S/(csinα+bsin2α)=2S/sinα(c+2bcosα)
同様に
t=2S/(bsinα+csin2α)=2S/sinα(b+2ccosα)
u=っSsinα/sinB=4SR/b(c+2bcosα)
=ac/(c+2bcosα)
w=ab/(b+2ccosα)
v=uw/2Rsinα=abcsinA/(b+2ccosα)(c+2bcosα)sinα
=abc(4cos^α−1)/(b+2ccosα)(c+2bcosα)
したがって,
BD:DC=u:(a−u)=c:2bcosα
→Dの重心座標は(0,2bcosα,c)
BE:EC=2ccosα:b
→Eの重心座標は(0,b,2ccosα)
直線ARの方程式はy:z=2bcosα:c
同様に,直線BRの方程式はAQ(=AE)の方程式を巡回的に回してz:x=c:2acosβ
したがって,交点Rの重心座標は
R(2acosβ,2bcosα:c)
と表される.同様に
P(a,2bcosγ,2ccosβ)
Q(2acosγ,b,2ccosα)
となる.
うまくまとめられるとよいのだが,どうも無理のようである.したがって,ΔPQRの中心の重心座標(x,y,z)はそのままの平均として次のように書かざるを得ない.
x=a/3[2cosβ/(2acosβ+2bcosα+c)+1/(a+2bcosγ+2ccosβ)+2cosγ/(2acosγ+b+2ccosα)]
y=b/3[2cosα/(2acosβ+2bcosα+c)+2cosγ/(a+2bcosγ+2ccosβ)+1/(2acosγ+b+2ccosα)]
z=c/3[1/(2acosβ+2bcosα+c)+2cosβ/(a+2bcosγ+2ccosβ)+2cosα/(2acosγ+b+2ccosα)]
===================================
【3】まとめ
a,b,cはよいがα=A/3,β=B/3,γ=C/3という3等分角のcosが入るので,これらはa,b,cに関する3次方程式の解でありうまくまとめられません.すなわち,α=A/3,β=B/3,γ=C/3のcosがa,b,cの代数関数ではあるが有理式にはなりそうもないため,有理的心にはならないというわけです.
===================================