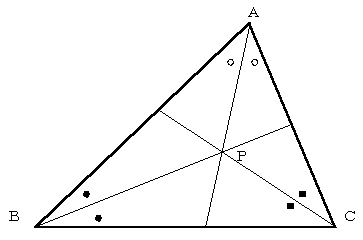
本コラムでは，中川宏さんの木工多面体を追跡レポートしてきたのであるが，その間，中川さんは木工多面体作家として着実に成長されたと思う．今回のコラムでは，中川さんがこの夏考察した初等幾何の定理についてまとめてみたい．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】はじめに三角形ありき

　三角形の内角の２等分線は１点で交わる（内心）．

　それに対して，三角形の内角の３等分線の交点は正三角形になる．

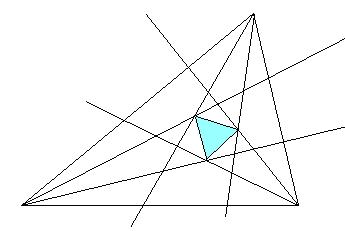
　これをモーレイの三角形と呼ぶが，モーレイの三角形が１８９９年，わずか１００年前に発見されたというのは驚きである．

　三角形のような簡単な図形が無数に未知の性質をもつというのはまことに不思議なことである．そこで，幾何学の基本形である三角形の性質について，もう一度見直してみたい．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

　三角形の５心とは，内心・傍心・重心・外心・垂心をさすが，これらは古くから知られていて，幾何学のバイブルと呼ばれるユークリッド「原論」にもその性質がいろいろ述べられている．三角形の内心は３辺への距離のうちで一番小さいものが最大になる点（マックスミニ点），外心は３頂点に至る最大距離が最小となる点（ミニマックス点），垂心は三角形に内接する三角形の周長が最小になる点（ファニャーノの問題，１７７５年），重心は３頂点に至る距離の２乗の和が最小となる点である．

　平面図形の中で３本またはそれ以上の直線が１点で交わっていることを主張する定理が共点定理であるが，たとえば，三角形の各頂点から対辺に引いた３つの中線や垂線は１点に会するなど，三角形の５心の存在は共点定理の例となっている．

　ちなみに，３頂点に至る距離の和が最小となる点をフェルマー点（シュタイナー点）という．この問題は１７世紀のフランスの数学者フェルマーがイタリアの物理学者トリチェリ，数学者カヴァリエリに出題したものとして有名な問題である．

　ここで，読者諸賢に問題を提出したい．

　［Ｑ］モーレイの三角形の重心はもとの三角形の何と一致するのだろうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】角から辺へ，２等分点ら３等分へ

　角の次は辺であるが，三角形の各頂点から対辺に引いた３つの中線は１点に会する（重心）．

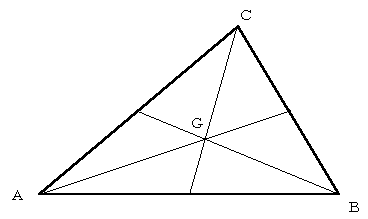
　２等分の次は３等分である．中点は辺の２等分点であるが，三角形の各頂点から対辺の３等分点に引いた線の交点は三角形になる．この三角形を仮に「縮小三角形」と呼ぶことにする．縮小三角形の面積は基の三角形の面積の１／７になるというのもよくある課題である．

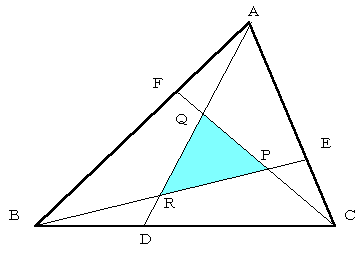
　正三角形の縮小三角形は正三角形であるが，中川宏さんの研究は任意の三角形の縮小三角形がもとの三角形と相似になる場合の問題である．

　［Ｑ］縮小三角形がもとの三角形と相似になることがあるか？　あるとすればどのような場合か？

　かなり面白く，数セミ・ノート欄に投稿してもよいような内容であるが，中川さん自身が部分的な解答を与え，一松信先生が「重心座標」を用いて完全に解いたことは，コラム「縮小三角形の問題」で紹介したとおりである．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

　次に辺の２等分点同士を結んでみると，どんな三角形でも各辺の中点をそれぞれ結んでやれば４等分することができることがわかるだろう（∵中点連結定理）．

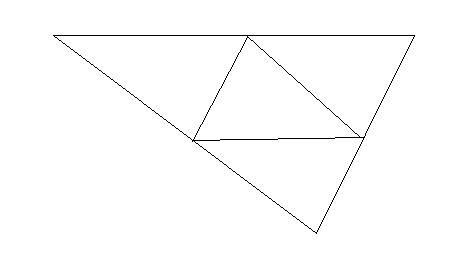
　一般にどんな三角形も４，９，１６，・・・，ｎ^2個に合同分割できるが，直角をはさむ二辺の比が１：ｎの直角三角形はｎ^2＋１個に合同分割できる．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

　三角形の各辺の３等分点を対頂点と結ぶと，中央部にできる小さな三角形はもとの三角形の１／７になるが，三角形の各辺の３等分点同士を結ぶとどうなるか？　任意の三角形の各辺の３等分点を下図のように結ぶと，三角形は３等分されることがわかる．

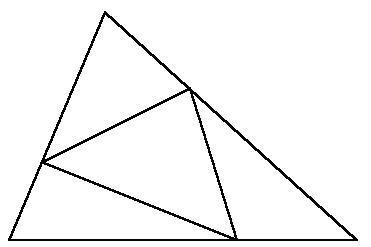
　一般に与えられた三角形の各辺を同じ倍率ｋで伸縮した位置に点をとって作った三角形の面積は，もとの三角形の面積の

　　Ｍ＝３ｋ^2−３ｋ＋１＝３（ｋ−１／２）^2＋１／４

倍になるから，

　　ｋ＝１／３　→　Ｍ＝１／３　　（３等分）

　　ｋ＝１／２　→　Ｍ＝１／４　　（４等分）

　　ｋ＝２／３　→　Ｍ＝１／３　　（３等分）

　　ｋ＝１　　　→　Ｍ＝１

　　ｋ＝２　　　→　Ｍ＝７　　　　（７等分）

となる．

　０＜ｋ＜１のときはもとの三角形より小さくなり，ｋ＝１／２のとき最小値１／４をとる．ｋ＞１のときはもとの三角形より大きくなり，ｋ＝２のときには７倍になるが，与えられた三角形の各辺を逆方向に延ばすと大きな三角形の対辺を１：２に内分する点と交わるのである．

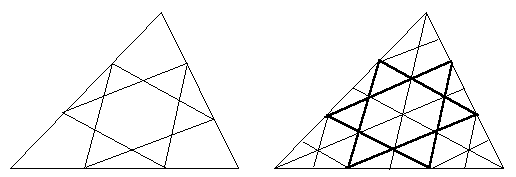
　また，下図のように３等分点を結んでダビデの星を作ってみると，ダビデの星では互いの辺を３等分し，面積はもとの三角形の面積の４／９に等しい．また，ダビデの星が重なった部分の６角形の面積はもとの三角形の面積の２／９，ダビデの星の面積の１／２に等しい．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝