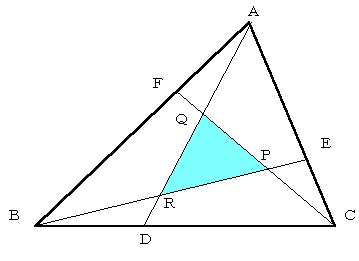
三角形ＡＢＣの各辺を１：λの比に順次内分した点Ｄ，Ｅ，Ｆとし，ＡＤ，ＢＥ，ＣＦの２本ずつの交点が作る三角計ＰＱＲを仮に「縮小三角形」と呼ぶことにする．

　正三角形の縮小三角形は正三角形であるが，中川宏さんの研究は任意の三角形の縮小三角形がもとの三角形と相似になる場合の問題である．かなり面白く，数セミ・ノート欄に投稿してもよいような内容である．

　一松信先生はこの問題を「重心座標」を使って計算されたそうであるから，小生も

　　［参］一松信「現代に活かす初等幾何入門」岩波書店，p10

を参考にしながら計算を試みたのであるが，重心座標系での相似形をどう表現するのかわからない．そこで，一松信先生に解説をお願いすることにした．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】縮小三角形がもとの三角形と相似になる場合

［Ｑ］縮小三角形がもとの三角形と相似になることがあるか？　あるとすればどのような場合か？

　中川宏さんはλ＝２で，三角形は直角三角形の場合を扱っているが，ここでは少し一般化し，λを１より大きい定数，三角形を任意の三角形として論じることにする．一松先生の結論を先にいうと

［Ａ］同じ向きに相似になるのは正三角形のときに限る．裏返しに相似になるのはパラメータａ，ｂ，ｃ，λの間に特別な関係がある場合である．たとえば，λ＝２のときは正三角形の半分（３辺の比が１：√３：２）のときがその一例である．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】証明

　以下，その証明をするが，重心座標による証明が簡便なので，それを使う．

［１］主要な点の重心座標はＤ（０，λ，１），Ｅ（１，０，λ），Ｆ（λ，１，０）

直線ＡＤ，ＢＥ，ＣＦの方程式はそれぞれｙ／λ＝ｚ，ｚ／λ＝ｘ，ｘ／λ＝ｙ．これらの交点としてＰ（λ，１，λ^2），Ｑ（λ^2，λ，１），Ｒ（１，λ^2，λ）　　　（いずれも重心座標の比のみ）

　ΔＰＱＲの面積／ΔＡＢＣの面積＝［λ，１，λ^2］／（λ^2＋λ＋１）^3

　　　　　　　　　　　　　　　　　［λ^2，λ，１］

　　　　　　　　　　　　　　　　　［１，λ^2，λ］

＝（λ−１）^2／（λ^2＋λ＋１）

　　　λ＝２なら１／７，λ＝３なら４／１３

　　［参］清宮俊雄「幾何学」科学新興新社，p11

　　　　　コラム「三角形のｎ等分（その２）」

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

［２］ΔＰＱＲの辺の長さは重心座標の長さの公式から次のようになる．

　　ＰＱ^2＝１／（λ^2＋λ＋１）^2×［λ−λ^2，１−λ，λ^2−１］のノルム

　＝（λ−１）^2／（λ^2＋λ＋１）×［−λ，１，λ＋１］のノルム

　＝（λ−１）^2／（λ^2＋λ＋１）×［ａ^2（λ＋１）＋ｂ^2λ（λ＋１）−ｃ^2λ］

　同様に

ＱＲ^2＝（λ−１）^2／（λ^2＋λ＋１）×［−ａ^2λ＋ｂ^2（λ＋１）＋ｃ^2λ（λ＋１）］

ＲＰ^2＝（λ−１）^2／（λ^2＋λ＋１）×［ａ^2λ（λ＋１）−ｂ^2λ＋ｃ^2（λ＋１）］

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

［３］ΔＰＱＲがΔＡＢＣと相似とすると，面積の関係から長さの相似比は　　　（λ−１）／√（λ^2＋λ＋１）

である．したがって，ＰＱ^2，ＱＲ^2，ＲＰ^2は

　　ａ^2，ｂ^2，ｃ^2／（λ^2＋λ＋１）

のいずれかに等しくなる．すなわち，共通因子を除いて，分子の［・・・］の内の量が

　　（ａ^2，ｂ^2，ｃ^2）（λ^2＋λ＋１）

のいずれかに等しくなる．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

［４］その形で方程式を作るが，同じ向きに相似なとき，それぞれの辺が最も近い辺に比例すると仮定すると

　　ａ^2（λ＋１）＋ｂ^2λ（λ＋１）−ｃ^2λ＝ａ^2（λ^2＋λ＋１）

　　−ａ^2λ＋ｂ^2（λ＋１）＋ｃ^2λ（λ＋１）＝ｂ^2（λ^2＋λ＋１）

　　ａ^2λ（λ＋１）−ｂ^2λ＋ｃ^2（λ＋１）＝ｃ^2（λ^2＋λ＋１）

→−ａ^2−λｂ^2＋（λ＋１）ｃ^2＝０

　　（λ＋１）ａ^2−ｂ^2−λｃ^2＝０

　−λａ^2＋（λ＋１）ｂ^2−ｃ^2＝０

３式を加えると，両辺とも同じ（ａ^2＋ｂ^2＋ｃ^2）（λ^2＋λ＋１）になるので，この３式は独立ではなく，ａ＝ｂ＝ｃを得る．

　右辺を巡回置換してもいずれも同様に計算してａ＝ｂ＝ｃに達する．すなわち自明な正三角形の場合以外にはあり得ない．

　裏返しに相似なとき，上述のＰＱ^2，ＱＲ^2，ＲＰ^2の式はそのままにして，第２式，第３式の右辺のｂ^2，ｃ^2を入れ換える．

第１式→−ａ^2−λｂ^2＋（λ＋１）ｃ^2＝０

第２式は右辺がｃ^2（λ^2＋λ＋１）であるから，整理すると

　　ａ^2＋λｂ^2−（λ＋１）ｃ^2＝０

となるが，これは第１式と同値である．

第３式は右辺がｂ^2（λ^2＋λ＋１）であるから，整理すると

　　−ａ^2−λｂ^2＋（λ＋１）ｃ^2＝０

となって，これも第１式と同値である．

　すなわち，この場合には相似条件式が同一の条件

　　ａ^2＋λｂ^2−（λ＋１）ｃ^2＝０

になる．もちろんａ＝ｂ＝ｃはこれを満足するが，それ以外にも多数の解がある．そしてそれが必要十分条件であり，実際に縮小三角形がもとの三角形と裏返しに相似になる．

例：λ＝２のとき，ａ＝１，ｂ＝２，ｃ＝√３（正三角形の半分）

同様にａ，ｂ，ｃを巡回置換すれば

　　−（λ＋１）ａ^2＋ｂ^2＋λｃ^2＝０

　　λａ^2−（λ＋１）ｂ^2＋λｃ^2＝０

という場合が生ずるが，これは単にａ，ｂ，ｃの順序を変えた（三角形を回した）ものにすぎない．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝