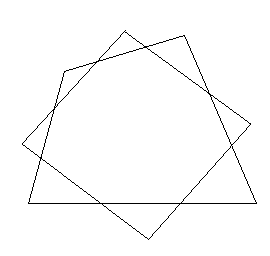
四角形の中点を結んでできる四角形は平行四辺形である．四角形を対角線で２つの三角形に分け，中点連結定理を適用すればこのことがわかる．したがって，四角形の対辺の中点を結ぶ線分は互いに他を２等分することもわかる．また，この小さい平行四辺形の面積はもとの四角形の面積の１／２，周長は対角線の長さの和に等しい．それでは，・・・

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】ウィッテンバウアーの平行四辺形

　もとの四角形の各辺の３等分点をとり，隣り合った３等分点を結ぶと８角形になるが，この線分の延長上にできる交点を結んでも平行四辺形ができる．この平行四辺形はウィッテンバウアーの平行四辺形と呼ばれる．

　もとの四角形の重心はウィッテンバウアーの平行四辺形の中心と一致する．

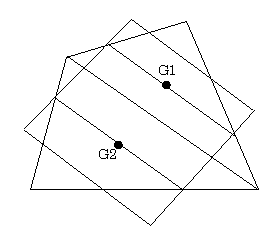
（証）四角形を対角線で２つの三角形に分けると，三角形の重心はもとの四角形とウィッテンバウアーの平行四辺形の交点を結ぶ線分の中点となる．したがって，もとの四角形の重心はウィッテンバウアーの平行四辺形の対辺の中点を結ぶ直線上にあることがわかる．同様に，もうひとつの対角線で２つの三角形に分けると，もとの四角形の重心はウィッテンバウアーの平行四辺形の中心と一致することが結論される．

　ウィッテンバウアーの平行四辺形の面積はもとの四角形の面積の８／９，周長は対角線の長さの４／３に等しい．また，もとの四角形とウィッテンバウアーの平行四辺形が重なった部分の８角形の面積はもとの四角形の面積の７／９，ウィッテンバウアーの平行四辺形の面積の７／８に等しい．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】四角形の重心は何処？

　三角形の３つの中線は一点で交わります．この交点が三角形の重心です．原点Ｏに対する三角形ＡＢＣの３頂点Ａ，Ｂ，Ｃの位置ベクトルをそれぞれａ，ｂ，ｃとすれば，重心の位置ベクトルは（ａ＋ｂ＋ｃ）／３となります．三角形の形をした均一な板の重心は３つの中線の交点，すなわち重心にあります．この点（一様な三角形の重心）は３つの頂点の重心（ａ＋ｂ＋ｃ）／３，すなわち三角形の頂点におかれた３つの等しい質量の中心（物理的重心）に一致します．

　一方，四面体ＡＢＣＤの３組の相対する辺の中点を結ぶ直線は１点で交わり，この交点の位置ベクトルは（ａ＋ｂ＋ｃ＋ｄ）／４となります．三角形と同様に，一様な四面体の重心はその４つの頂点の重心（ａ＋ｂ＋ｃ＋ｄ）／４と一致します．一様な棒の重心は両端の間の距離を１：１に，三角形の重心は中線を２：１に，四面体の重心は頂点と向かいあう面の重心との距離を３：１に内分します．すなわち，四面体の重心は１つの面の重心から対頂点に引いた直線の１／４の点にあります．４次元以上でもこの規則性が失われることはありそうもなく同様に類推されます．三角形の重心の性質は四面体に遺伝するのです．

　ところが，四角形ＡＢＣＤの重心Ｇにはうまい性質がありません．三角形からの類推で，四角形の重心は（ａ＋ｂ＋ｃ＋ｄ）／４となるような気もします．しかし，これは４点Ａ，Ｂ，Ｃ，Ｄに等しい質量がある場合の重心であって，密度一様な板の場合には当てはまりません．

　多角形の各頂点に同じ重さのおもりをつけたときの釣り合いの位置を「頂点の重心」と呼ぶことにすると，任意の四角形の４辺の中点は平行四辺形の頂点になりますから，ＡＢの中点とＣＤの中点とを結ぶ直線とＡＤの中点とＢＣの中点を結ぶ直線との交点は四角形の頂点の重心（ａ＋ｂ＋ｃ＋ｄ）／４に当たります．この点は２対角線の中点を結ぶ線分を１：１に内分します．ここで，ｄ→ｃすなわち三角形の１つの頂点の付近をちょっと切り取った限りなく三角形に近い四角形を考えると

　　（ａ＋ｂ＋ｃ＋ｄ）／４→（ａ＋ｂ＋２ｃ）／４

ですから，（ａ＋ｂ＋ｃ）／３には一致せず，（ａ＋ｂ＋ｃ＋ｄ）／４は重心ではないことがわかります．三角形では頂点の重心は普通の意味の重心（ａ＋ｂ＋ｃ）／３に一致しますが，四角形ではそうではないのです．一般にベクトルａk に同一の質量があるとき，この質点系の重心はベクトル（ａ1 ＋ａ2 ＋・・・＋ａn ）／ｎで表されます．三角形については，これは均質な板の重心と一致しますが，ｎ≧４では均質な板の重心と頂点のみの質点系の重心とは一致しません．それでは，四角形の薄板の重心はどこに位置するのでしょうか．

　四角形ＡＢＣＤを対角線ＡＣで，三角形ＡＢＣと三角形ＣＤＡに分けると△ＡＢＣの重心Ｇ1 と△ＣＤＡの重心Ｇ2 を結ぶ直線上で，各々の面積を逆比に内分する点に重心Ｇがあります．対角線ＢＤで分けると△ＡＢＤの重心Ｇ3 と△ＢＣＤの重心Ｇ4 を結ぶ直線との交点が重心Ｇとなります．何とか式で表現できないかと考えて，次のような結果を得ました．

　重心Ｇの位置ベクトルをｇ，三角形ＡＢＣの面積を△ＡＢＣ，四角形ＡＢＣＤの面積を□と書くことにすると，

ｇ＝｛△ＡＢＣ（ａ＋ｂ＋ｃ）＋△ＣＤＡ（ｃ＋ｄ＋ａ）｝／３□・・・（１）

ｇ＝｛△ＡＢＤ（ａ＋ｂ＋ｄ）＋△ＢＣＤ（ｂ＋ｃ＋ｄ）｝／３□・・・（２）

（１）＋（２）を実行すれば

ｇ＝｛（２□−△ＢＣＤ）ａ＋（２□−△ＣＤＡ）ｂ＋（２□−△ＤＡＢ）ｃ＋（２□−△ＡＢＣ）ｄ｝／６□

　＝（ａ＋ｂ＋ｃ＋ｄ）／３−｛△ＢＣＤ・ａ＋△ＣＤＡ・ｂ＋△ＤＡＢ・ｃ＋△ＡＢＣ・ｄ｝／６□

問題はａ，ｂ，ｃ，ｄに対して対称的ですから，重点の式はａ，ｂ，ｃ，ｄを取り替えても変わらないものでなければなりません．ベクトルの外積を用いると△ＡＢＣは，１／２（ｂ−ａ）×（ｃ−ａ）＝１／２（ｂ×ｃ＋ｃ×ａ＋ａ×ｂ）で与えられますから，ｇの対称式が得られます．

　四角形の重心Ｇを作図によって求めるためには，４辺の中点が必要になります．あるいは，四角形の各辺の３等分点をとり，隣り合った等分点を結ぶと平行四辺形ができますが，四角形の重心Ｇはその平行四辺形の中心と一致します．四角形の重心の作図法については，黒田俊郎「コマと重心」（数学セミナー・リーディングス「新しい高校数学の展望」（日本評論社）やコクセター「幾何学入門」（明治図書）にも記述があります．なお，３本の均一な針金でできた縁だけの三角形（いわば一次元の三角形）の重心は，三角形の各辺の中点を結んだ三角形の内心に位置します．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝