幾何学では相似や合同を鏡映（反転）を含めて同じものとみなすのが一般的だそうだが，平面充填の周期性・非周期性を意識すると，鏡映を区別することも意味を持つ場合があるだろう（中川宏）．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

（イ）２等分

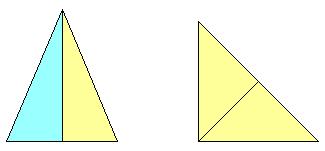
　左の図のように，二等辺三角形は一般に合同図形に２等分出来るが，２等分片はもとの三角形と相似ではなく，かつ相互に鏡映である．ただひとつ，右の図のような直角二等辺三角形だけは，２等分片がもとの図形と相似であり，かつ鏡で区別されない合同図形となる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

（ロ）３等分

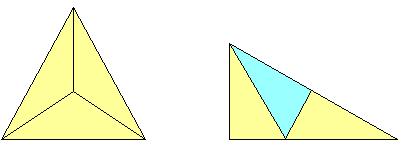
　正三角形を左の図のように３等分すると，分割片は鏡で区別されないが，元の図形とは相似ではない．他方，右の図のように，正三角形の半分の直角三角形を３等分すると，元の図形と相似になるが，３つのうち１つは鏡映図形となる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

（ハ）４等分

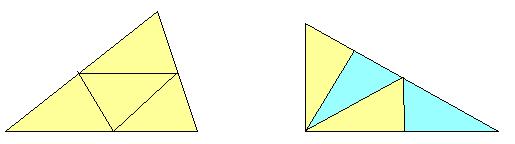
　一般に三角形は相似で合同な図形に４等分出来るが，それらは鏡で区別されない．しかし，右の正三角形の半分の直角三角形の場合は２：２で鏡映図形に分割することもできる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

（ニ）５等分

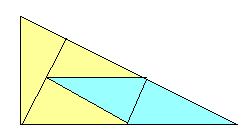
　直角をはさむ２辺の比が１：２の直角三角形は相似で合同な図形に５等分できるが，それらは３：２の比で鏡映図形となる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

（ホ）６等分

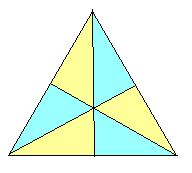
　正三角形は合同に６等分出来るが，それらは元の三角形と相似ではない．また，３：３で鏡映図形になる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝