定規とコンパスだけで正３角形、正４角形、正６角形、正８角形が作図できることは簡単にわかりますが，辺の数５，７，９の場合はどうでしょうか．正５角形は古代ギリシャにおいて作図可能であることが発見されました．となれば，次に正７角形・正９角形の作図は？と考えるのは自然な成り行きでしょう．ところが，かのアルキメデスでさえも正７角形・正９角形の作図に成功しなかったといわれています．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】近似的な内接正１３角形の作図

　内接正多角形の作図は画家であり建築家であるレオナルド・ダ・ヴィンチの関心を惹きました．しかし，彼でさえ近似的な内接正七角形の作図を正確なものと思っていたようです．

　ところで，正方形の辺の２等分点を使った作図が黄金比あるいは正五角形の作図に繋がっているのですが，正１７角形の作図には４等分点が使われているそうです．中川宏さんはそれをもとにして近似的な内接正１３角形の作図を考案されました．彼の発想は以下のようなものです．

(1)直角をはさむ二辺の比が１：ｎの直角三角形はｎ^2＋１等分できる．

(2)ｎ＝２のとき正五角形，ｎ＝３のとき正十角形の作図が可能

(3)ｎ＝４のとき正１７角形の作図が可能．

(4)ｎ＝５のとき正２６角形の作図と関係するならば，正１３角形も描けるはず・・・．

　正１３角形は作図不可能であることが証明されているのですが，近似的な作図法は存在するはずです．そこで，

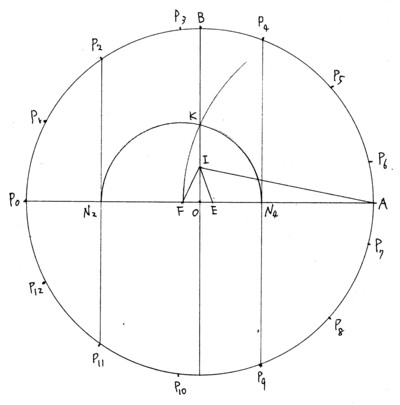
(1)半径ＯＢの５等分点Ｉをとる．

　　∠ＯＩＥ＝∠ＡＩＯ／４，∠ＦＩＥ＝４５°

(2)半径ＸＯＢを切る点をＫとする．

(3)Ｆを中心として，Ｋを通る円がＰ0Ａと交わる点をＮ2，Ｎ4とする．

(4)直径Ｎ2Ｎ4の円の接線が直径ＡＰ0の円と交わる点が正１３角形の４頂点となる．

　中川さんの近似作図法で正１７角形の場合と違っているのは点Ｉと点Ｋの取り方だけだそうです．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】正１７角形の作図

　辺数３，４，５，６，８，１０，１２，１５，１６の正多角形は作図できますが，辺数７，９，１１，１３，１４の正多角形は作図できないことから，正１７角形もそうであろうと推察されます．ところが，１７９６年，ガウスは１９才のときに正１７角形の作図を思いつき，のみならず，ｎが素数の正ｎ角形について，ｎ＝２^(2^m)＋１が素数の場合に限り定規とコンパスだけで作図可能であることを発見しています．

　正７角形も正９角形も作図できないのに，まさか正１７角形が作図できるとはと思うのが普通なのでしょうが，このことを用いると，ｍ＝０のとき正３角形，ｍ＝１のとき正５角形，ｍ＝２のとき正１７角形となり，作図可能であることがわかります．当然，ずっと面倒になるでしょうが，正２５７角形（ｍ＝３），正６５５３７角形（ｍ＝４）も作図可能です．

　２^(2^m)＋１の形の素数をフェルマー素数といいます．フェルマー素数はガウスによって１世紀にわたる眠りから覚まされ，数論と幾何学に新たな美しさを吹き込んだことになります．フェルマーはこの型の数がすべて素数だと勘違いしていて必ず素数を与える式として考え出されたのですが，ｍ＝５のときは素数ではなく，現在，ｍ＝０，１，２，３，４の５個以外にフェルマー素数はみつかっていません．６番目のフェルマー素数の探索がコンピュータを使ってなされていますが，はたして本当に存在するのでしょうか．

　アルキメデスは円柱とそれに内接する球の体積比が３：２であることを発見した記念に，自分の墓の上に円柱の形をした記念碑をおくように遺言したといわれています．アルキメデスと同じように，ガウスは正１７角形を墓石に彫るよう遺言しています．このことはガウス自身がその発見をいかに重視したかを物語っています．数々の大発見をしたガウスですが，１９才の青年がアルキメデスをもってしてもできなかった古代ギリシア以来２０００年の謎を解いたのですから，まさに驚きとしかいいようがありません．この正１７角形の作図は彼を本格的に数学の道に入らせるきっかけとなったといわれています．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝