３次元の平行多面体（フェドロフの平行多面体５種）がすべて同一の素片（１種）で組み立てられるというのが「平行多面体元素定理」である．確かに３次元の場合がうまくいきすぎているようで，４次元の場合，全部を数え上げることは容易ではない．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】長菱形十二面体

　ところで，フェドロフの平行多面体５種のうち，立方体，正六角柱，菱形十二面体，切頂八面体はよくわかるが，長菱形十二面体がよくわからないという人は多い．

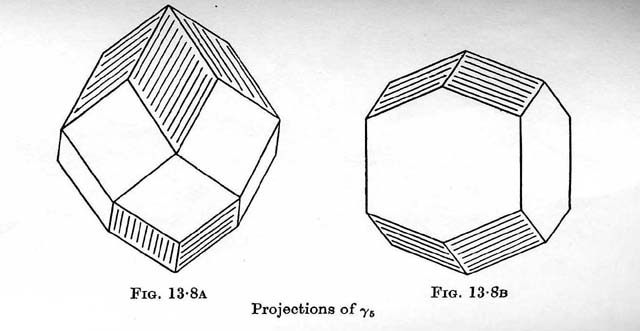
　長頂八面体は六角形を４枚並べて，屋根と底に菱形４枚をはめた形である．菱形十二面体，切頂八面体がそれぞれ面心立方格子，対心立方格子のボロノイ領域であることはよく知られているが，長菱形十二面体がどのような格子に所属しているのかよくわからないからであろう（おそらく底心格子だろう）．

　コクセターの"Regular Polytopes", 1978年のDover版のp257に載っている図では菱形は白銀菱形（鋭角ａｒｃｃｏｓ（１／３））ではなく，鋭角がａｒｃｃｏｓ（１／６）〜８０°というかなり正方形に近い形である．もちろん六角形も正六角形ではなく，２つの対頂角がａｒｃｃｏｓ（−２／３）〜１３１°という値をとる．

［補］黄金菱形の鋭角はａｒｃｃｏｓ（τ^2−１）／（τ^2＋１）

黄金２乗菱形の鋭角はａｒｃｃｏｓ（τ^4−１）／（τ^4＋１）

白銀２乗菱形の鋭角はａｒｃｃｏｓ（３／５）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】雑感

　たたし，その前後を読んでも，なぜコクセターが√（５／６），√（１／６）といった半端な値のときの充填形を選んでいるのかよくわからなかった．

　小生にはいくつか菱形多面体に関するマイ未解決問題がある．たとえば，菱形１３２面体の菱形の形など・・・．わかった人は教えてほしい．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝